Next: 4.4 Source terms Up: 4 Métodos en diferencias Previous: 4.2.5 Extensions of classical
1. Numerical grid:
2. Time update:
![]() Conservation form algorithm
Conservation form algorithm
In practice: 2nd or 3rd order time accurate conservative Runge-Kutta schemes (Shu and Osher 1989)
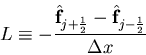
3. Numerical fluxes:
Approximate Riemann solvers: Roe, HLLE, Marquina
Explicit use of the characteristic information of the system
Flux Formula
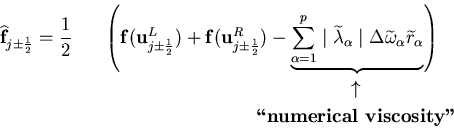
![]() ,
, ![]() : left and right ``reconstructed" variables
: left and right ``reconstructed" variables
![]() : eigenvalues
: eigenvalues
![]() : jump of characteristic variables
: jump of characteristic variables
![]() : right-eigenvectors
: right-eigenvectors
4. Cell reconstruction:
Piecewise constant (Godunov) or linear (``MUSCL" scheme, van Leer) interpolation
procedures of ![]() from cell centers to cell interfaces. Higher-order
procedures also available: parabolic (PPM, Colella and Woodward) or hyperbolic
(PHM, Marquina)
from cell centers to cell interfaces. Higher-order
procedures also available: parabolic (PPM, Colella and Woodward) or hyperbolic
(PHM, Marquina)
with
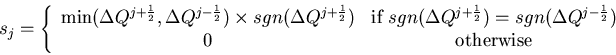
with