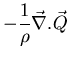Next: 2.4 Flujo Compresible Unidimensional Up: 2 Dinámica de fluidos Previous: 2.2 Ecuaciones de la
![]() Admitimos la existencia de gradientes de velocidad.
Admitimos la existencia de gradientes de velocidad.
![\fbox{\parbox[b]{3.95in}{
\begin{displaymath}
d \vec{F} = - {\cal P} d \vec{\Sigma}
\end{displaymath}}}](img159.png)
![]()
![]() es un tensor (tensor de presiones), función de
la presión termodinámica y del gradiente de velocidades.
es un tensor (tensor de presiones), función de
la presión termodinámica y del gradiente de velocidades.
![]() En coordenadas cartesianas,
En coordenadas cartesianas, ![]() es la i-componente de la
fuerza sobre la unidad de superficie orientada en la j-dirección.
es la i-componente de la
fuerza sobre la unidad de superficie orientada en la j-dirección.
![]() En general:
En general:
| (20) |
![]() es la matriz unidad, y
es la matriz unidad, y ![]() es el tensor de tensiones:
es el tensor de tensiones:
![\fbox{\parbox[b]{3.95in}{
\begin{displaymath}
{\cal S}_{ij} = 2 \mu \displaystyl...
..._{kk} \delta_{ij} \right)
+ \xi {\cal D}_{kk} \delta_{ij}
}
\end{displaymath}}}](img165.png)
![]()
![]() : primer coeficiente de viscosidad (shear viscosity)
: primer coeficiente de viscosidad (shear viscosity)
![]()
![]() : segundo coeficiente de viscosidad (bulk viscosity)
: segundo coeficiente de viscosidad (bulk viscosity)
![]()
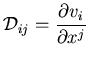 (tensor de deformaciones).
(tensor de deformaciones).
![]()
![]() (Expansión).
(Expansión).
![]()
![]() (tensor de distorsiones).
(tensor de distorsiones).
![]() (traza nula: deformación sin cambio de volumen)
(traza nula: deformación sin cambio de volumen)
Ecuación de Euler extendida:
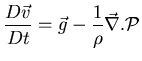
![\fbox{\parbox[b]{4.95in}{
{\bf Ecuaci\'on de Navier-Stokes:}
\begin{displaymath...
...{3} \mu}{\rho} \right) \vec{\nabla}
(\vec{\nabla} . \vec{v})
\end{displaymath}}}](img172.png)
![]() Fluido incompresible :
Fluido incompresible :
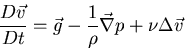 |
(21) |
![]()
![]() es el coeficiente de viscosidad cinemática
es el coeficiente de viscosidad cinemática
![]()
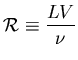 es el número de Reynolds
es el número de Reynolds
![]()
![]() : longitud y velocidad características
: longitud y velocidad características
![]()
![]()
![]()
![]() efectos de viscosidad despreciables
efectos de viscosidad despreciables
![]() Aplicando el operador rotacional a N-S:
Difusión de la vorticidad
Aplicando el operador rotacional a N-S:
Difusión de la vorticidad
| (22) |
Ecuación de la energía extendida:
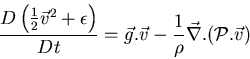 |
(23) |
Disipación de energía ![]() Despejando
Despejando
![]() , e introduciendo el tensor de tensiones:
, e introduciendo el tensor de tensiones:
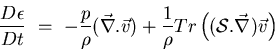 |
(24) |
![]() El primer término a la derecha
El primer término a la derecha ![]() expansión
adiabática
expansión
adiabática
![]() El segundo término a la derecha
El segundo término a la derecha ![]()
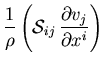
es un ritmo de generación de energía -calor- porefectos de viscosidad.
![]() Si hubiese flujo de calor,
Si hubiese flujo de calor, ![]()
![]()