Next: 2.4.2 Invariantes de Riemann Up: 2.4 Flujo Compresible Unidimensional Previous: 2.4 Flujo Compresible Unidimensional
![]() Perturbaciones adiabáticas (
Perturbaciones adiabáticas (
![]() )
en un fluido perfecto, homogéneo y en reposo
)
en un fluido perfecto, homogéneo y en reposo
![\fbox{\parbox[b]{3.5in}{
\begin{displaymath}
\left(\Delta - \frac{1}{c_s^{2}} \f...
...partial^{2}}{\partial t^{2}}
\right) \delta \rho = 0
\end{displaymath}}}](img187.png)
![]() A primer orden:
A primer orden:
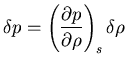
![]()
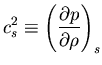
![]()
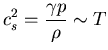 , para gas ideal
, para gas ideal
![]()
![]() satisface la misma ecuación de ondas.
satisface la misma ecuación de ondas.
![]() Estado inicial: irrotacional e isoentrópico (en un fluido perfecto)
Estado inicial: irrotacional e isoentrópico (en un fluido perfecto)
![]() el estado perturbado es irrotacional
el estado perturbado es irrotacional
![]()
![]()
![]()
![]() y cada componente de
y cada componente de ![]() satisfacen la misma
ecuación de ondas.
satisfacen la misma
ecuación de ondas.
![]() Flujo unidimensional, en coordenadas esféricas (ondas esféricas):
Flujo unidimensional, en coordenadas esféricas (ondas esféricas):
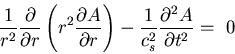 |
(25) |
![]() Solución general: superposición de ondas esféricas convergentes y divergentes:
Solución general: superposición de ondas esféricas convergentes y divergentes:
| (26) |