Next: 2.4.3 Ondas Simples Up: 2.4 Flujo Compresible Unidimensional Previous: 2.4.1 Teoría lineal de
![]() Flujo adiabático, unidimensional:
Flujo adiabático, unidimensional:
![]() ,
,
![]() ,
,
![]()
| (27) |
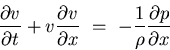 |
(28) |
| (29) |
![]() Ecuación de estado:
Ecuación de estado:
![]()
![]()
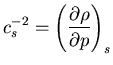
![]() Variables primitivas:
Variables primitivas:
![]()
![]() (31) es un sistema cuasilineal (subíndices: variable respecto de la cual
se calcula la derivada parcial), donde
las matrices
(31) es un sistema cuasilineal (subíndices: variable respecto de la cual
se calcula la derivada parcial), donde
las matrices ![]() y
y ![]() dependen de U:
dependen de U:
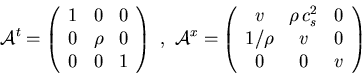
Sea la combinación lineal de las dos primeras ecuaciones en (31):
![]()
![]()
![]()
![]()
![]()
![]()
Imponemos la condición de que las funciones presión y velocidad aparezcan
derivadas a lo largo de la misma dirección (la correspondiente a una
cierta curva ![]() ):
):
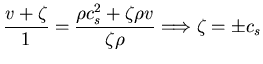 |
|||
| (31) |
![]() Operadores:
Operadores:
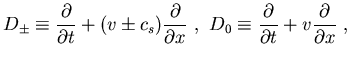
Las ecuaciones en (31) se han reescrito, en (2.4.2) y (2.4.2), de
modo que las derivadas
![]() son direccionales según las
curvas integrales (
son direccionales según las
curvas integrales (
![]() ,
, ![]() , respectivamente) de las
ecuaciones diferenciales:
, respectivamente) de las
ecuaciones diferenciales:
![\fbox{\parbox[b]{3.5in}{
\begin{displaymath}
{\cal C}_{\pm} : \displaystyle...
...cal C}_{0} : \displaystyle{\frac{dx}{dt} = v }
\end{displaymath}}}](img222.png)
![]() Los campos de curvas
Los campos de curvas
![]() son las características del sistema.
son las características del sistema.
![]() Las ecuaciones en (2.4.2) y (2.4.2) son ecuaciones diferenciales ordinarias sobre cada
una de las curvas características
Las ecuaciones en (2.4.2) y (2.4.2) son ecuaciones diferenciales ordinarias sobre cada
una de las curvas características
![]() método de las características
método de las características
![]() En un diagrama espacio-tiempo
En un diagrama espacio-tiempo
![]() dominio de dependencia,rango de influencia
dominio de dependencia,rango de influencia
![]() Flujo isoentrópico
Flujo isoentrópico
![]() La (2.4.2) es redundante
La (2.4.2) es redundante
![]()
![]()
![]()
![]()
![]() . En este caso, los invariantes de Riemann:
. En este caso, los invariantes de Riemann:
son constantes a lo largo de
![]() :
:
![]()
![]() Gas ideal isoentrópico:
Gas ideal isoentrópico:
![]()
| (32) |