Next: 2.4.4 Ondas de Choque Up: 2.4 Flujo Compresible Unidimensional Previous: 2.4.2 Invariantes de Riemann
![]() Estado Constante: Región del plano x-t donde los valores de todas las
magnitudes que definen el fluido son constantes.
Estado Constante: Región del plano x-t donde los valores de todas las
magnitudes que definen el fluido son constantes.
![]() Flujo isoentrópico
Flujo isoentrópico
![]() velocidad y presión constantes
velocidad y presión constantes
![]() Flujo isoentrópico
Flujo isoentrópico
![]() Las características son rectas
Las características son rectas
![]() La frontera de un estado constante (en el plano
La frontera de un estado constante (en el plano ![]() ) son características
) son características
![]() Onda Simple: Región del plano x-t donde uno de los invariantes de Riemann(
Onda Simple: Región del plano x-t donde uno de los invariantes de Riemann(![]() )
es constante.
)
es constante.
![]() En una onda simple tal que
En una onda simple tal que![]() sea
constante, las
sea
constante, las
características
![]() son líneas rectas.
son líneas rectas.
![]() Las regiones adyacentes a los estados constantes son ondas simples.
Las regiones adyacentes a los estados constantes son ondas simples.
![]() Las partículas del fluido que atraviesan una onda simple,
Las partículas del fluido que atraviesan una onda simple, ![]() , lo hacen de derecha a izquierda (de izquierda a derecha); en consecuencia, ven viajar la onda simple,
, lo hacen de derecha a izquierda (de izquierda a derecha); en consecuencia, ven viajar la onda simple,
![]() de izquierda a derecha (de derecha a izquierda)
de izquierda a derecha (de derecha a izquierda)
![]() De la definición de
De la definición de ![]() en (2.4.2)
en (2.4.2)
![]()
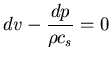
![]() Las ondas simples
Las ondas simples ![]() verifican:
verifican:
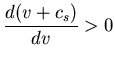
![]() De la definición de
De la definición de ![]() en (2.4.2)
en (2.4.2)
![]()
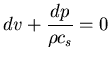
![]() Las ondas simples
Las ondas simples ![]() verifican:
verifican:
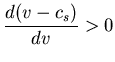
![]() Onda de Rarefacción: Onda simple en la que la presión (densidad) disminuye al atravesarla.
Onda de Rarefacción: Onda simple en la que la presión (densidad) disminuye al atravesarla.
![]() Si la onda simple,
Si la onda simple, ![]() es de rarefacción
es de rarefacción
![]()
![]() y
y ![]() disminuyen
(
disminuyen
(![]() y
y ![]() aumentan)a lo largo de las trayectorias
de las partículas del fluido.
aumentan)a lo largo de las trayectorias
de las partículas del fluido.
![]() Onda de Compresión: Onda simple en la que la presión (densidad) aumenta al atravesarla.
Onda de Compresión: Onda simple en la que la presión (densidad) aumenta al atravesarla.
![]() Si la onda simple,
Si la onda simple, ![]() es de compresión
es de compresión
![]()
![]() y
y ![]() aumentan
(
aumentan
(![]() y
y ![]() disminuyen)a lo largo de las trayectorias
de las partículas del fluido.
disminuyen)a lo largo de las trayectorias
de las partículas del fluido.
![]() Onda Simple Centrada: La familia de características que son líneas rectas
confluyen todas en un punto.
Onda Simple Centrada: La familia de características que son líneas rectas
confluyen todas en un punto.
![]() Sea
Sea ![]() una onda simple de rarefacción centrada.
una onda simple de rarefacción centrada.
![]() Obtengamos la solución para toda la región
Obtengamos la solución para toda la región
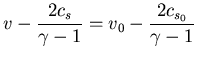
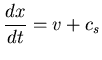
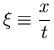 , de las dos últimas
ecuaciones se obtienen
, de las dos últimas
ecuaciones se obtienen
![\fbox{\parbox[b]{3.5in}{
\begin{displaymath}
v = \displaystyle{\frac{1...
... }
\left[ \xi - v_0 \right] +
\frac{2 c_{s_0}}{\gamma + 1}}
\end{displaymath}}}](img251.png)
La solución para el flujo es la misma en todos los puntos (x,t) tales que ![]()
![]() Flujo autosemejante.
Flujo autosemejante.