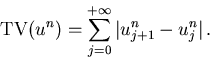Son algoritmos de alto orden que tienen variación total
estable. La variación total de una solución en  ,
TV(
,
TV(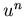 ), se define como
), se define como
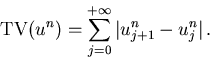 |
(126) |
Un esquema numérico se dice que es TV-estable si TV(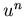 )
está acotada para cualquier
)
está acotada para cualquier 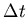 en cualquier instante y
para cualquier dato inicial. El interés en los métodos
TV-estables radica en el hecho de que para esquemas numéricos en
forma conservativa con flujos numéricos consistentes, la
estabilidad TV es una condición suficiente de convergencia.
en cualquier instante y
para cualquier dato inicial. El interés en los métodos
TV-estables radica en el hecho de que para esquemas numéricos en
forma conservativa con flujos numéricos consistentes, la
estabilidad TV es una condición suficiente de convergencia.
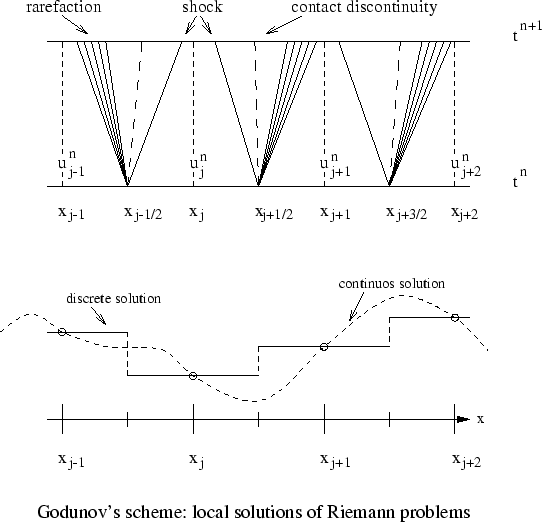
El alto orden se consigue mediante funciones polinómicas
monótonas conservativas que interpolan las soluciones
aproximadas o los flujos numéricos en las celdas numéricas.
Algoritmos de reconstrucción bien conocidos son el MINMOD (segundo
orden), PPM (tercer orden) o los métodos ENO (que mantienen la
variación total acotada).
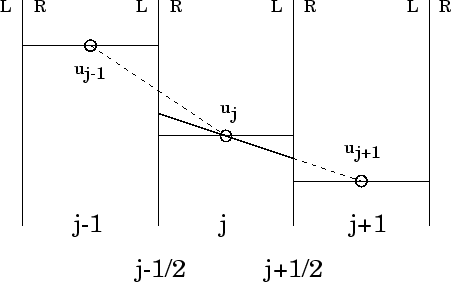
Reconstrucción MINMOD: en cada celda numérica se efectúa una
interpolación lineal con la menor de las pendientes con las celdas
contiguas.