Model of evolution of interchange among countries
Rafael
Pla-López
Departament de Matemàtica Aplicada
Universitat de València
Abstract We study the evolution of the proportions of interchange among countries by tending to equalize the production and the consumption of each country. We find that the convergence of this evolution to an equilibrium depends positively on the delay in this tendency. |
Introduction
Surplus/deficit of the balance of payment of each country is a main problem in the present world. The actions to overcome it repercusses on the whole economical processes of the society, and specifically on the employment.
We worked in a collective study sponsored by Generalitat Valenciana through Conselleria de Cultura, Educació i Ciència inside the framework of Pla Valencià de Ciència i Tecnologia (Project GV97-TI-D5-20) to simulate the evolution of unemployment through different approaches [Caselles, 1996; Caselles et al., 1999a; Caselles et al., 1999b]. I specifically worked in a minimalist approach of successive disaggregation of variables to build series of models of growing complexity.
Traditional approaches, which don’t consider the evolution of the variables, aren’t accurate to study economical process, like the unemployment, which are essentially dynamic. So, the main lines of our work used System Dynamics [Aracil, 1992; Forrester, 1968; Forrester, 1971].
In the minimalist approach, we basically simulate the evolution with temporally discrete lineal dynamical systems: we modelize that a variable X tends toward a variable Y with a delay tA through the relation
![]()
with tA ³ 1. Naturally, if tA = 1, then X(t+1) = Y(t). We express this relation by means of
X|tA ® Y
On the other hand, models of On-Only-Country are insufficient to simulate economical evolutions in a globalized world. Of course, it is usual to consider outputs and inputs from abroad (nobody would think that a model of a closed system were today realistic), but this approach has difficult to integrate the internal dynamics of other countries, plunged in the "environment". Specifically, it is usual to consider constant outputs from this environment. But it is not realistic, especially in relation to the balance of payments: this balance is also altered for the actions from other countries in order to overcome its own surplus/deficit. Thus, the interaction and accumulation of these actions have to be considered.
Global Models modelize the whole world, by considering different parts of the Earth, which usually aggregate a set of countries [Meadows et al., 1985; Castellar, 1998]. Nevertheless, to modelize interchanges we have to work with each country, and can only aggregate a set of countries, like the European Union, which are economic units for interchange.
Of course, a model with more than a hundred of
countries would be very complex. But, in a first step, we are
interested in the general dynamic of the interchange, and so we
will work with abstract models.
Basic Model
In a first step, Atur 0 ("Atur" is the Catalan word for Unemployment), we have initially considered one only Social System and worked with global means. We used variables as
- QP = Quantity of Production
- QC = Quantity of Consumption
which are not separated by sectors.
The Model doesn’t treat explicitly with means of payment and monetary relations, although it implicitly requires units of measurement to treat homogeneously Production and Consumption of different sectors.
We supposed that Quantity of Production tends toward Quantity of Consumption with a certain delay,
QP|t1® QC
In a second step, Atur 1 disaggregates the System in a set of m Social System (countries), although Production inside of each System continues without to be disaggregated.
So, we suppose that Quantity of Production of each System-Country i, QP(i), tends toward an ideal value QPO(i) which depends on its demand from different countries through some coefficients f(i,j), which expresses the proportion of the Consumption of the System-country j which generates demand from the System-country i.
Hence,
QP(i) | t1® QPO(i)
QPO(i)
= Sj
f(i,j)·QC(j)
Si f(i,j)=1
- Changing the interchange.
Of course, in equilibrium QP(i) = QP0(i) , and therefore
QP(i) = Sj f(i,j)·QC(j)
But we should also to suppose that equilibrium requires a balanced interchange for every System-country, QP(i) = QC(i) . In this case,
Sj f(i,j)·QC(j) = QC(i) ,
and therefore QC(i) has to be a self-vector of the matrix f(i,j) with self-value equal to one.
Thus, the version Atur 1.4 of the Model includes an evolution process of the coefficients of interchange f(i,j) in case of unbalanced interchange.
Because f(i,j) have to fulfil the condition Si f(i,j)=1, the matrix Aij = f(i,j) – dij will fulfil Si Aij = 0, and therefore, by being its rows lineally dependent, its Determinant will value zero, which is precisely the condition for that f(i,j) admit one as a self-value. Therefore, the only problem is that QC(i) would be the corresponding self-value, by accurately adapting the coefficients f(i,j) .
We can do it through an iterative process to search a solution of the corresponding system of equations
SjQC(j)·f(i,j) = QC(i).
With a iteration of iteration de Jacobi we have
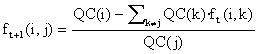
Note that the relation Si f(i,j)=1 is conserved in this iteration. In effect,
Si ft+1(i,j) = 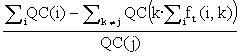 =
= 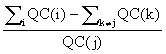 =
=![]()
Now then, this iteration haven't to converge (the corresponding matrix won't fulfil, in general, the condition of convergence of being strictly diagonally dominant by rows).
See you the particular case of m = 2 Systems-countries. In this case the relation will be
f(0,0)·QC(0) + f(0,1)·QC(1) = QC(0),
which, by applying the condition f(0,0) + f(1,0) = 1, becomes f(0,1)·QC(1) = f(1,0)·QC(0).Hence, if we define
![]() ,
,
the condition for that QC(i) fulfilled the condition of equilibrium with f(i,j) will be A = 1.
Now then, if we apply the indicated iteration we will have
ft+1(0,1)= ft(1,0)·![]() ,
,
ft+1(1,0)=
ft(0,1)· ![]() ,
,
and so
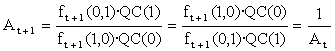
Hence, if A¹ 1 initially we will have a succession (A, 1/A, A, 1/A,...) which, of course, won't converge.
Observe you the practical meaning of this process: if each System-country directly adapts its coefficients f(i,j) to equilibrate its interchange with the other, the result is not this equilibrium, but a series of periodic oscillations.
Slowing the change.
To avoid these oscillations we could slow the iteration by introducing a delay tf, so that, with
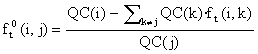
the coefficients f(i,j) with j ¹ 1; i tended toward this value with a delay tf,
ft(i,j)|tf ® f0t(i,j), and so
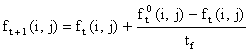 =
=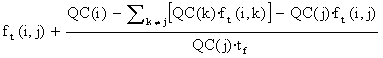 =
=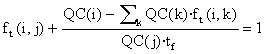
We can verify that the relation Si f(i,j) = 1 is conserved:
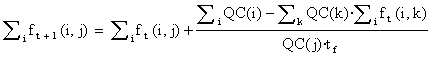 =
=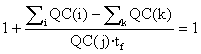
In the case m = 2 we will have
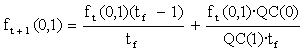
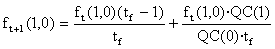
and therefore
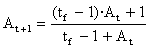
Naturally, if tf =1 were fulfilled we would newly obtain![]() . And if tf ® +¥ , At+1 ® At
. And if tf ® +¥ , At+1 ® At
If we want that At+1=1, then we will have to require
(tf – 1)At+1=tf – 1 + At,
which is equivalent to
(tf – 2)(At – 1) = 0,
which will be fulfilled if At = 1 or tf = 2. So then, the delay tf = 2 always permits to obtain the coefficients of equilibrium in one only step. We could say that the Systems-countries have "splitted the difference" in its search of its equilibrium of interchange. And, in general, if tf ³ 2 we can anticipate a convergence of the iteration without oscillations.
We will demonstrate that we can generalise this result to the general case of m Systems-countries, so that tf = m carries to obtain the convergence in one step.
In effect,
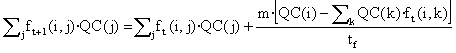 =
=
![]()
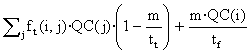
Hence, if tf = m the condition of equilibrium ![]() will be fulfilled.
will be fulfilled.
In general, the residue will value
Rt+1= åj ft+1(i,j)·QC(j)
– QC(i) =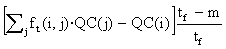
Therefore,
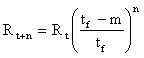
and the condition of convergence of the iteration
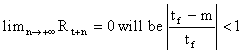 .
.
So that, if tf ³ m the iteration will
converge without oscillations. If tf < m , the
condition of convergence will be m-tf < tf ,
that is to say, tf < ![]() : if
: if ![]() < tf < m , the residue will change
of sign in each iteration by being approximate to zero.
< tf < m , the residue will change
of sign in each iteration by being approximate to zero.
If tf = ½ (like in the case m = 2,
tf=1), Rt+1 = –Rt , and the
iteration will produce periodic oscillations without converging.
If tf < ![]() ,
, ![]() and
the iteration will diverge: the residue will oscilate between
plus and minus infinite.
and
the iteration will diverge: the residue will oscilate between
plus and minus infinite.
Observe that, in the limit, if tf ® +¥ , then Rt+1 @ Rt , to be annulled the evolution (ft+1(i,j) @ ft(i,j)).
In the Model Atur 1.4 we have took tf = m·t1 , the evolution toward the equilibrium of interchange were gave by
fOt(i,j) = 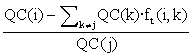
and the coefficients ft (i,j) tended toward fOt(i,j) with a delay tf = mt1 , and so
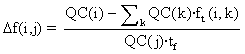 .
.
- Conclussion
According to our model, a hard adjustment carry to increase unbalanced economical state, and a soft adjustment is more efficient.
Our model could so explain the financial and social convulsions which have been generated by policies of hard adjustment of the balance of payment, and suggests the convenience of smooth policies, by searching little and slow changes of this balance, especially in a global world with many countries in interaction.
Of course, these policies will only be effective if its application is generalised in the world. Therefore, the intercommunication in international economical forums becomes essential in order to achieve a balanced interchange between the different countries.
Particularly, in the conditions of our model,
and if we consider annual cycles, the better results would be
obtained if each country programmed its adjustment with a delay
of so many years as the number of countries which interchange: in
this way, every them would be able to arrive to a balanced
interchange in one year.
References
[Aracil, J., 1992] Introducción a la Dinámica de Sistemas, pp.262 ss. Alianza Editorial. Madrid.
[Caselles, A., 1996] A systemic Approach to Unemployment Control, Third European Congress on Systems Sciencie, 487-491. Edizioni Kappa. Roma.
[Caselles, A., Ferrer, L., Martínez de Lejarza, I., Pla, R., Temre, R., 1999a] Control del Desempleo por Simulación. Universitat de València. València.
[Caselles, A., Ferrer, L., Pla, R., Temre, R., Martínez de Lejarza, I., 1999b] Simulation for Unemployment Control. Diputació de València, Àrea d'Informàtica. València.
[Castellar Busó, V., 1998] Un model sistèmic d'evolució social sostenible, pp. 3-30, 169-194. Departament de Matemàtica Aplicada. Universitat de València. València.
[Forrester, J.W., 1968] Principles of Systems. Wright-Allen Press. Cambridge.
[Forrester, J.W., 1971] World Dynamics. Wright-Allen Press. Cambridge.
[Meadows, D.H., Robinson, J.M., 1985] The Electronic Oracle: Computer Models and Social Decisions. Wiley. Chichester.