RECTA DE REGRESIÓN X/Y (M.C.O.)

ir a script de regresión

Pretendemos obtener, ahora la regresión lineal que nos explique la variable X en función de los valores de Y.El procedimiento de obtención será, en todo análogo, al anterior, pero ahora la función de regresión a obtener será:

     x* = a' + b' Y con la pretensión de que:

  S S (x_i - (a'+b' y_j) ) ².n_ij sea mínima .

Habrá que encontrar los valores de los parámetros a' y b' que minimizan esa expresión.Es decir que anulan simultaneamente las derivadas parciales de la función:

    y (a' , b' )=S S (x_i - (a'+b' y_j) ) ².n_ij : (Sistema de ecuaciones normales)

= 0	2S S (xi -a'-b' yj ) . nij (-1)= 0
= 0	2S S [ xi -a'-b' yj ) . nij ].[-S S yj nij ] = 0

S S xi nij =a'S S nij +b' S S yj nij
S S yj xi nij = a S S xi nij +bS S xi2 nij

(*1')

                                    restando la segunda ecuación por la primera multiplicada por -y, quedará:

Sxy=b' S2y (*2')

de forma que de (*1') y de (*2') se concluye que los valores de a' y b'que minimizan los cuadrados de los residuos y que, por tanto son los parámetros del ajuste mínimo-cuadrático serán:

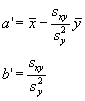
                                La ecuación de la recta de regresión Y/X quedará, por lo tanto como:

De (*1) , o de la propia ecuación de la recta se deduce que la recta de regresión de Y/X pasa por el centro de gravedad de la distribución .

Otra expresión alternativa de la recta de regresión de regresión Y/X es: