se verifica que para cualquier valor de K
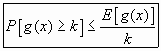
veamos.
TEROREMA DE MARKOV Y ACOTACIÓN DE CHEBYSHEV
(volver a esperanza matemática)
Tras conocer el concepto de operador esperanza , podemos adentrarnos en el denominado teorema de Markov y la consecuente acotación de Chebyshev , que nos servirá para establecer aproximaciones/acotaciones para la media e incluso para diversos valores de la variable .Planteadas la posibilidades que conllevan estos teoremas pasamos a desarrollarlos brevemente.
Teorema de Markov.
Dada una variable aleatoria X con
función de densidad
asociada f(X) y una función "No" negativa de esa variable
![]()
se verifica que para cualquier valor de K
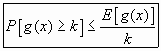
veamos.
Dada la Variable aleatoria X y su función
![]()
Podríamos tener su representación grafica de la siguiente forma.
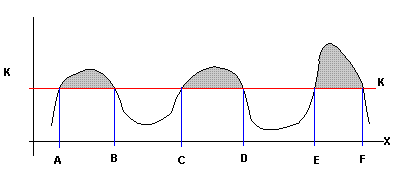
En el gráfico se aprecia que S es el conjunto de valores para los que g(x)≥K , así
![]() por otro lado tendremos que:
por otro lado tendremos que:
![]() dado que S
son los valores en que la función es mayor que K
dado que S
son los valores en que la función es mayor que K
tendremos también que ![]()
![]()
y así tendríamos que
![]()
ya que cuando x pertenece a S se cumple que g(x)≥K
evidentemente tendremos que
![]()
Consecuencia del teorema tendremos la siguiente expresión derivada
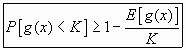
Acotación de Chebyshev.
Partiendo del teorema de Markov y tras establecer algunos cambios matemáticos se puede establecer la denominada "acotación de Chebyshev.
En base a la consecuencia directa del teorema de Markov que
hemos anteriormente hemos establecido ,
es decir
![]()
En la que realizamos los siguientes cambios:
A)
![]() que es evidentemente una función no negativa siguiendo las pautas del teorema de
Markov.
que es evidentemente una función no negativa siguiendo las pautas del teorema de
Markov.
B)
![]() que sigue siendo una determinada constante
que sigue siendo una determinada constante
En base a estos cambios la anterior desigualdad de Markov quedaría.
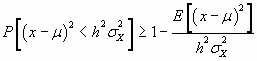
dado que ![]()
tendríamos consecuentemente que
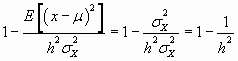
por lo que
![]() o lo
que es lo mismo
o lo
que es lo mismo
![]() que es la expresión de la acotación de Chebyshev
que es la expresión de la acotación de Chebyshev
Esta expresión es susceptible de transformarse en otras de carácter más operativo, Así
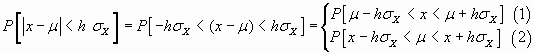
Por la primera (1) tendríamos
![]() que nos
explicita una cota mínima para la probabilidad de que la variable se encuentre
dentro de los valores de un intervalo centrado en la media.
que nos
explicita una cota mínima para la probabilidad de que la variable se encuentre
dentro de los valores de un intervalo centrado en la media.
Por la segunda (2) tendríamos
![]() que indica la
probabilidad mínima con la que la media se encuentra dentro de un intervalo
centrado. Esta expresión es de gran importancia para llevar a cabo inferencias
sobre la media de la población de una variable aleatoria cuando se desconoce
como se distribuye ésta , siempre y cuando nos sea conocida la varianza de dicha
población
que indica la
probabilidad mínima con la que la media se encuentra dentro de un intervalo
centrado. Esta expresión es de gran importancia para llevar a cabo inferencias
sobre la media de la población de una variable aleatoria cuando se desconoce
como se distribuye ésta , siempre y cuando nos sea conocida la varianza de dicha
población