FUNCIÓN CARACTERÍSTICA
La función característica de la distribución de probabilidad de una
variable aleatoria x se define como :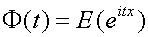
Así pues se trata de una función parámetrizada sobre una variable real auxiliar t
que queda definida como el valor esperado o esperanza
de la función compleja exp ( itx ) en donde i es la
unidad imaginaria 
Propiedades
- Al estar definida sobre el plano complejo existirá siempre
- En virtud del teorema de inversión de Fourier la función característica define
unívocamente la distribución, de ahí su nombre de función característica ,
permitiendo la obtención unívoca de la función de densidad o de cuantía
según las expresiones:
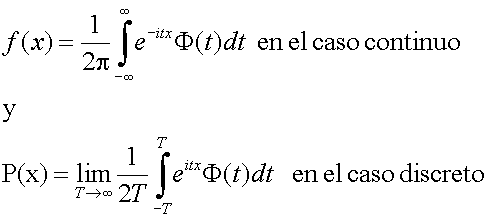
- Derivando sucesivamente la Función característica en el punto t = 0 se generan los
sucesivos momentos ordinarios de los distintos
órdenes según la expresión:
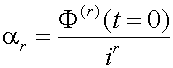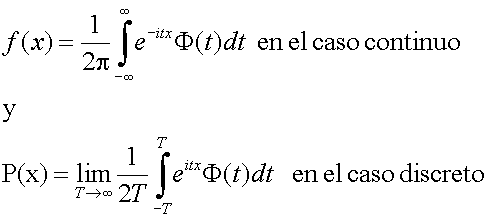
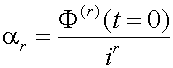de forma análoga a como ocurre e el caso de la
función generatriz de momentos.