VARIABLE ALEATORIA         

DISTRIBUCIÓN DE PROBABILIDAD. PROBABILIDAD INDUCIDA.
VARIABLE ALEATORIA DISCRETA
VARIABLE ALEATORIA CONTINUA
FUNCIÓN DE DISTRIBUCIÓN EN VARIABLE DISCRETA
FUNCIÓN DE DISTRIBUCIÓN EN VARIABLE CONTINUA
FUNCIÓN DE DENSIDAD    (PROPIEDADES)  (GRÁFICO)
ESPERANZA DE UNA VARIABLE ALEATORIA
TEOEMA DE MARKOV, ACOTACION DE CHEBYSHEV
OPERADOR ESPERANZA
MOMENTOS
OPERADOR VARIANZA
FUNCIÓN GENERATRIZ DE MOMENTOS
FUNCIÓN CARACTERÍSTICA
TEOREMA DE LOS MOMENTOS

VARIABLE ALEATORIA DISCRETA:

Una variable aleatoria es discreta cuando su campo de variación (dominio de definición) está constituido por un conjunto finito o infinito numerable de valores posibles. Cada suceso de W se corresponde con un valor .

Ej 1 : ante el experimento : lanzar un dado diez veces se aleatoriza de forma que la variable aleatoria X = nº de ases que se obtengan : X ={0,1,2,3,4,5,6,7,8,9,10} (v.a. discreta de orden finito)

Ej 2 : ante el experimento : contemplar los coches que pasen por un tramo de carretera se aleatoriza de forma que la variable aleatoria X = nº de coches que pasen: X={0,1,2,3,...} ( X= N ) (v. a. discreta de orden infinito)

Si la variable aleatoria es discreta, cada valor de los pertenecientes al campo de variación se corresponderá con un suceso del álgebra de sucesos.(lo que permitirá después asignar probabilidades a cada valor ).

Una variable aleatoria discreta es el modelo teórico de una variable estadística discreta (con valores sin agrupar).

Una variable aleatoria discreta es aquella cuya función de distribución es escalonada.

VARIABLE ALEATORIA CONTINUA .

Es aquella cuyo dominio de definición (campo de variación) es un intervalo (compacto) de la recta real , una unión de varios intervalos , o la totalidad de la recta real.(Por lo tanto los valores definidos de la variable aleatoria son un conjunto infinito no numerable .) El álgebra de sucesos del que surge debe contener un número infinito no numerable de sucesos ,cada uno de ellos se corresponderá con alguno de los (infinitos) intervalos incluidos en el campo de definición.

Ejemplo 3. ante el experimento : contemplar los coches que pasen por un tramo de carretera se aleatoriza de forma que la variable aleatoria X =tiempo que hay que esperar hasta que pase un coche X = [0,µ [ ,es decir X=R+

En el caso continuo no podremos hacer corresponder a los valores (puntuales) con sucesos de álgebra de sucesos, la correspondencia se establecerá entre sucesos del álgebra e intervalos pertenecientes al campo de variación de la variable .En consecuencia no podremos asignar probabilidades a los valores de la variable, sino sólo a intervalos.

Una variable aleatoria continua es el modelo teórico de una variable estadística continua (agrupada por intervalos ).

Una variable aleatoria continua es aquella cuya función de distribución es continua.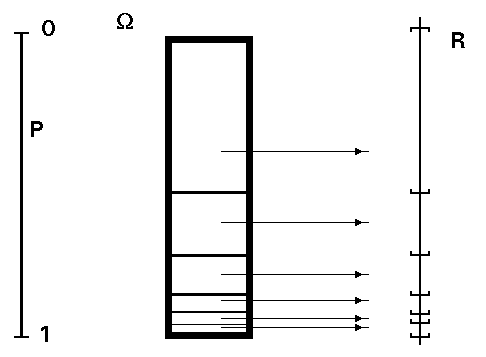

DISTRIBUCIÓN DE PROBABILIDAD. PROBABILIDAD INDUCIDA.

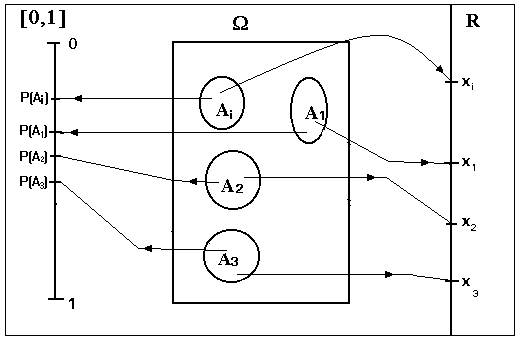
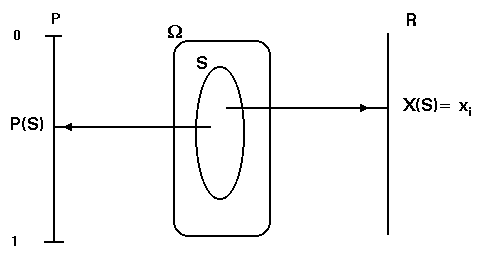
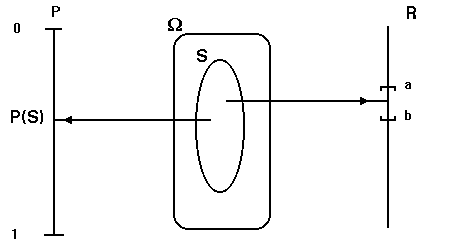
Si ,por un lado, el espacio de resultados está asociado, a través de la probabilización con el intervalo [0,1], de forma que cada suceso tiene asociada una probabilidad; y, por otra parte, cada suceso está asociado con un valor (caso discreto) o con un intervalo (caso continuo) de la recta real (variable aleatoria) , a través de la aleatorización; podremos asignar, entonces, probabilidades a los valores ( o a los intervalos ) de la variable aleatoria.Esto es lo que se conoce como probabilidad inducida (sobre la v.a.).

" a Î X(W ) : Px (a) = P( X^-1(a))

donde a será un valor puntual de la variable aleatoria si es discreta, o un intervalo ,si es continua.

De esta forma, la masa total (unitaria) de probabilidad puede repartirse (distribuirse) entre los valores definidos de la variable aleatoria (si es discreta) o entre los distintos intervalos (si es continua).

Si consideramos, entonces la variable aleatoria, junto con su asignación de probabilidad (inducida), estamos ante una DISTRIBUCIÓN DE PROBABILIDAD ( X ,PX).

Función de distribución en distribuciones de variable discreta:

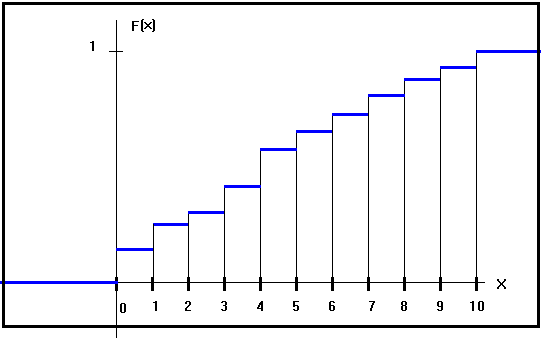
Puede observarse que:

· Presenta un perfil escalonado,produciendose un salto en cada uno de los valores definidos de la variable aleatoria.Es continua por la derecha, pero no por la izquierda.

· La cuantía de cada salto es precisamente la probabilidad en ese punto, la función de cuantía.

· Es semejante al DIAGRAMA ACUMULATIVO de una distribución de frecuencias de valores sin agrupar.

· Entre cada dos puntos (de los definidos) no hay probabilidad (y por tanto no se acumula).

Función de distribución en una distribución de variable continua.

En una distribución de variable continua se induce probabilidad sobre todos los infinitos intervalos que integran el campo de definición de la variable .En consecuencia ante cualquier incremento de la variable (por pequeño que sea) le corresponderá un incremento de la probabilidad de que se va acumulando, lo que hará que la función de probabilidad acumulada,la función de distribución tenga que ser continua en todos lo puntos del campo de definición de la variable.Es esta la razón de que se llamen distribuciones continuas, ya que acumulan de forma continua su probabilidad.

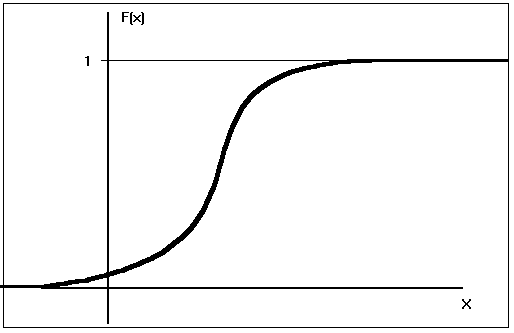
Podemos observar cómo:

· La función de distribución es continua por ambos lados (absolutamente continua), acumulando la variable probabilidad de manera continuada desde que comienza su campo de variación hasta que termina (acumulando la masa total ,1).

· Tiene un perfil similar al del POLÍGONO ACUMULATIVO de una distribución de frecuencias de valores agrupados.Coincidiría con él si se tratara de intervalos infinitésimo.

Función de densidad (distribuciones continuas)

En el caso de una distribución continua se va acumulando probabilidad de manera continua, ante cualquier incremento de la variable a lo largo de su campo de variación.Pero los puntos singulares no tienen asociada probabilidad.(no hay probabilidad en un punto)(No tiene sentido pensar en una función de cuantía).

Sin embargo cualquier intervalo (por pequeño que sea sí tiene asociada una probabilidad).Y dado un intervalo cualquiera podemos definir la DENSIDAD MEDIA DE PROBABILIDAD en ese intervalo como el cociente entre el incremento de probabilidad que se ha acumulado y el incremento producido en la variable:

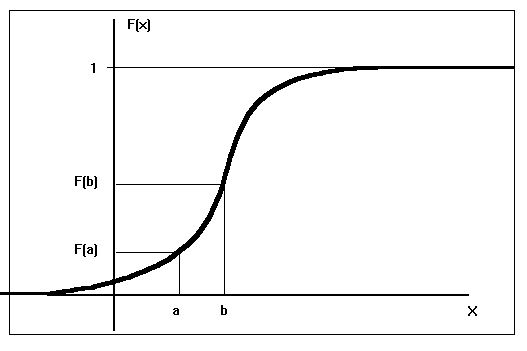
Densidad media de probabilidad en [a,b]

y para un intervalo [x,x+D x] sería:

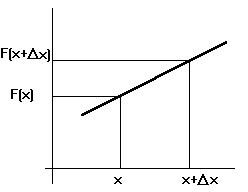
D.M.P([x,x+D ])

Propiedades de la función de densidad:

1. La función de densidad es "no negativa " para todo valor de x: " x: f(x) ³ 0

2. P(X£ x) =F(x)

3.

4. P( a £ X £ b) =P( a <X £ b ) =P( a £ X <b) =P(a < X <b) =

5. limx® -¥ f(x) =limx® +¥ f(x) =0

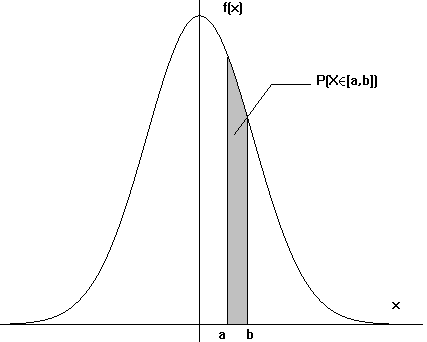
ESPERANZA DE UNA VARIABLE ALEATORIA

La esperanza de una variable aleatoria se define como:

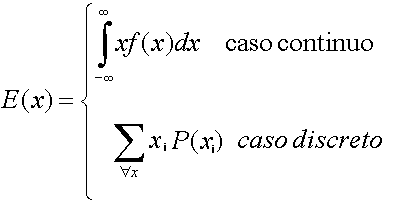
La esperanza de la variable aleatoria coincide con el centro de gravedad de su distribución de probabilidad y se le puede considerar su promedio, de hecho es la media de la distribución.

E(x)=m= media de la distribución.

OPERADOR ESPERANZA

El concepto de esperanza puede generalizarse para cualquier función g(x) de la variable aleatoria x así tendríamos que 

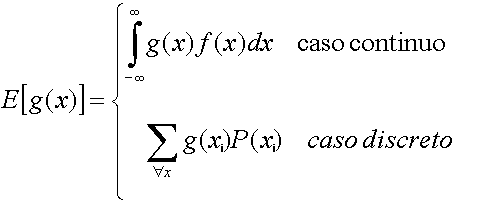
Propiedades:

1. La esperanza de una constante es la propia constante
2. La esperanza de una función lineal es la misma función lineal de la esperanza.La linealidad los operadores integral y sumatorio garantizan el cumplimiento de esta propiedad.

OPERADOR VARIANZA

Tambien la varianza puede generalizarse, como en el caso de la esperanza y así se define la varianza de una función g(x) de la variable aleatoria x como:

D²(g(x))= E[(g(x)-E(g(x)))²]

Sus principales propiedades son:

1. La varianza de una función constante es cero
2. La varianza de una función lineal g(x)= a + bx es : D²(a + bx )= b².D²(x)

MOMENTOS DE LA DISTRIBUCIÓN

Análogamente a como ocurría en las distribuciones de frecuencias pueden definirse los momentos ordinarios y centrales de una distribución de probabilidad, en esta ocasión en función del operador esperanza:

Momento ordinario de orden r :

Momento central de orden r :

Entre los principales momentos de una distribución destacan la media, que es el momento  ordinario de orden 1 y la varianza  que es el momento central de segundo orden:

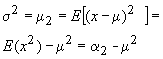
Como en el caso de la estadística descriptiva la varianza es el principal indicador de dispersión de la distribución de probabilidad.

TEROREMA DE MARKOV Y ACOTACIÓN DE CHEBYSHEV

(volver a esperanza matemática)

Tras conocer el concepto de operador esperanza , podemos adentrarnos en el denominado teorema de Markov y la consecuente acotación de Chebyshev , que nos servirá para establecer aproximaciones/acotaciones para la media e incluso para diversos valores de la variable .Planteadas la posibilidades que conllevan estos teoremas pasamos a desarrollarlos brevemente.

Teorema de Markov.

Dada una variable aleatoria X con función de densidad asociada f(X) y una función "No" negativa de esa variable
se verifica que para cualquier valor de K
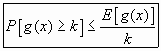
veamos.

                    Dada la Variable aleatoria X y su función   

Podríamos tener su representación grafica de la siguiente forma.

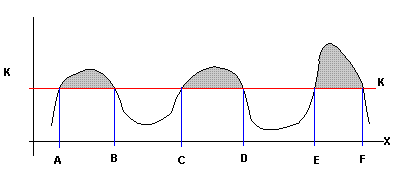
                      En el gráfico se aprecia que S es el conjunto de valores para los que g(x)≥K , así

                              por otro lado tendremos que:

dado que S son los valores en que la función es mayor que K

                   tendremos también que

              y así tendríamos que

                          ya que cuando x pertenece a S se cumple que g(x)≥K

                            evidentemente tendremos que            

Consecuencia del teorema tendremos la siguiente expresión derivada

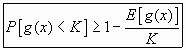
Acotación de Chebyshev.

Partiendo del teorema de Markov y tras establecer algunos cambios matemáticos se puede establecer la denominada "acotación de Chebyshev.

En base a la consecuencia directa del teorema de Markov que hemos anteriormente hemos establecido ,
es decir  

En la que realizamos los siguientes cambios:

A)     que es evidentemente una función no negativa siguiendo las pautas del teorema de Markov.

B)             que sigue siendo una determinada constante

En base a estos cambios la anterior desigualdad de Markov quedaría.

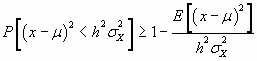
               dado que

tendríamos consecuentemente que     

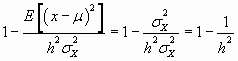
                por lo que    o lo que es lo mismo

         que es la expresión de la acotación de Chebyshev

Esta expresión es susceptible de transformarse en otras de carácter más operativo, Así

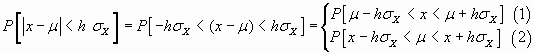
Por la primera (1) tendríamos que nos explicita una cota mínima para la probabilidad de que la variable se encuentre dentro de los valores de un intervalo centrado en la media.

Por la segunda (2) tendríamos que indica la probabilidad mínima con la que la media se encuentra dentro de un intervalo centrado. Esta expresión es de gran importancia para llevar a cabo inferencias sobre la media de la población de una variable aleatoria cuando se desconoce como se distribuye ésta , siempre y cuando nos sea conocida la varianza de dicha población

FUNCIÓN GENERATIZ DE MOMENTOS

La función generatriz de momentos ( F.G.M.) de la distribución de probabilidad de una variable aleatoria x se define como:.
Así pues se trata de una función parámetrizada sobre una variable real auxiliar t que queda definida como el valor esperado o esperanza de la función exp ( tx )

Propiedades

1. No siempre se puede garantizar su existencia, aunque para la mayoría de la distribuciones de probabilidad de uso habitual sí existe.
2. Cuando existe, caracteríza unívocamente la distribución de probabilidad , análogamente a la función característica. De forma que si las distribuciones de dos variables aleatorias x e y son tales que sus dos F.G.M.,j_x y j_y , son idénticas j_x =j_y entonces las distribuciones de las variables x e y también son idénticas.
3. Derivando sucesivamente la F.G.M. en el punto t=0 se generan los sucesivos momentos ordinarios según la expresión: este resultado se conoce como teorema de los momentos
4. Si se transforma una variable aleatoria x en otra y mediante una función lineal: y= a+bx , la F.G.M. de la distribución de y obedece a la expresión:

              propiedad especialmente importante para   comprobar la linealidad de la distribución normal

FUNCIÓN CARACTERÍSTICA

La función característica de la distribución de probabilidad de una variable aleatoria x se define como :

Así pues se trata de una función parámetrizada sobre una variable real auxiliar t que queda definida como el valor esperado o esperanza de la función compleja   exp ( itx ) en donde i es la unidad imaginaria

Propiedades

1. Al estar definida sobre el plano complejo existirá siempre
2. En virtud del teorema de inversión de Fourier la función característica define unívocamente la distribución, de ahí su nombre de función característica , permitiendo la obtención unívoca de la función de densidad o de cuantía según las expresiones:

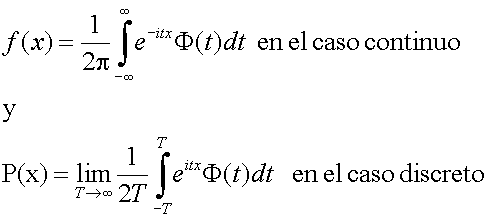
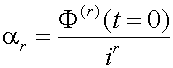3. Derivando sucesivamente la Función característica en el punto t = 0 se generan los sucesivos momentos ordinarios de los distintos órdenes según la expresión: de forma análoga a como ocurre e el caso de la función generatriz de momentos.

TEOREMA DE LOS MOMETOS MOMENTOS

La derivada r-sima de la F.G.M   en el punto t=0 coincide con el momento ordinario de orden r de la distribución.

en efecto, si desarrollamos en serie la función exponencial tendremos:

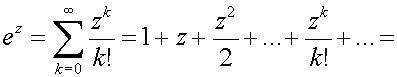
aplicándolo a z = tx, tendremos:

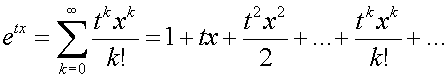
y por lo tanto la F.G.M. puede expresarse como:

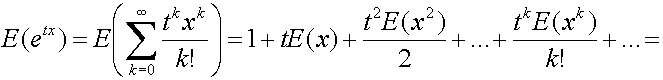
y de esta forma las sucesivas derivadas quedarían como:

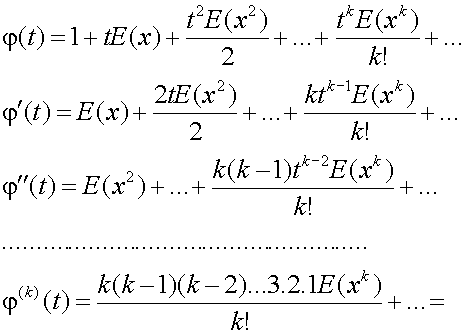
y por último calculando estas derivadas en el punto t= 0 es facil ver que: