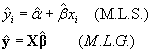
ESTIMACIÓN DEL MODELO Y PREDICCIÓN PUNTUAL
Nos plantemos, en primer lugar construir un estimador del modelo (esto es , del valor teórico de yi) con la pretensión fundamental de obtener a partir del modelo estimado predictores puntuales de y para situaciones no observadas (supuestos ciertos valores de x).
Vamos buscando un estimador del tipo:
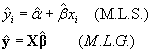
Empleando el método de máxima verosimilitud para obtener los E.M.V. de a,b,s en M.L.S. tendremos que:
La función de densidad de cada dato yi será:
![]()
y por tanto la f. de verosimilitud para el
conjunto de los n datos : ![]()
Tomando logaritmos e igualando a cero las derivadas parciales con respecto a a,b,s obtendríamos los tres E.M.V:
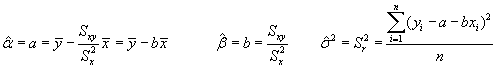
Es decir, se obtiene como resultado de la estimación máximo verosímil que los estimadores de los parámetros son los coeficientes de la regresión mínimo cuadrática y el estimador de la varianza de la perturbación, la varianza residual muestral.
Quedando el modelo estimado como: ![]()
y el predictor para un periodo
extramuestral: ![]()
Puede probarse que el E.M.V. del vector de parámetros b del M.L.G.también coincide con el vector obtenido por ajuste mínimo cuadrático:
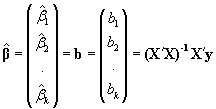
Siendo también la varianza residual muestral el E.M.V. de la varianza de la perturbación