CUESTIONES PREVIAS SOBRE LA REGRESIÓN (MUESTRAL) MÍNIMO-CUADRÁTICA:

Recordemos que el método de ajuste por "mínimos cuadrados "a una

recta y= a + b x se basaba en obtener como coeficientes a,b aquellos valores que :

min j (a,b)= min S (y_i- a - bx_i)²

y que el resultado de tal ajuste acababa siendo:

Igualmente para el caso multidimensional la ecuación de ajuste mínimo cuadrático y = b₀+b₁x₁+. . . +b_kx_k

que matricialmente puede expresarse (si la extendemos para los n datos disponibles) como: y= Xb

la podremos obtener

min j ( b_0,b_1, . . . ,b_k) = min S (yi- b₀- b₁x₁- . . . - b_kx_k)²

esto es: min j ( b)= min (y - Xb )' (y - Xb )

de forma que el vector de coeficientes b que nos dará la ecuación de ajuste mínimo-cuadrático será tal que igualará a cero la derivada parcial de j ( b) con respecto a b :

j ( b)= (y - Xb )' (y - Xb ) = y'y - (Xb)'y - y'(Xb)+(Xb)'(Xb) =

= y'y - b'X'y - y'X b + b'X'X b = y'y - 2 b'X'y + b'X'X b

por lo que la derivada parcial de j ( b) con respecto a b acaba siendo:

-2 X'y + 2 X'X b que si la igualamos a cero nos dará la solución del ajuste mínimo-cuadrático:

-2 X'y + 2 X'X b= 0 Û b= (X'X)^-1 X'y

de forma que el vector de coeficientes que nos da el ajuste a un hiperplano que minimiza la suma de los cuadrados de los residuos es:

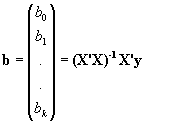
es facil comprobar que en el caso de la regresión simple los coeficientes de la recta de regresión mínimo-cuadrática verifican también esa relación:

en efecto en el caso de la regresión simple tenemos:

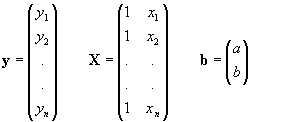
de manera que X'X será:

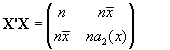
y su inversa (X'X )^-1 =

y por otro lado X'y sera: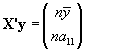

por lo que el vector (X'X)-1 X'y acaba siendo:

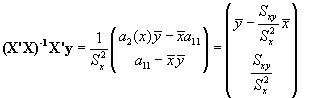
es decir los valores de los coeficientes a y b que ya conocemos.

RECORDEMOS, en otro orden de cosas,que la VARIANZA RESIDUAL era uno de los indicadores de la calidad del ajuste tanto en el caso de la REGRESIÓN SIMPLE como de la LA MÚLTIPLE, y se definía como: S_r²= 1/n · S (y_i- a -bx_i)² en el caso de la R.simple

S_r²= 1/n · S (yi- b₀- b₁x₁- . . . - b_kx_k)²

en el caso de la R. múltiple

y matricialmente S_r²= 1/n · (y- Xb)'( y-Xb)

En el caso de la regresión simple : S_r²= S_y²(1 - r²) = S_y² - r².S_y²

y en el caso de la regresión múltiple: S_r²= S_y² (1 - R²) = S_y² - R².S_y²

donde r y R son respectivamente el coeficiente de correlación entre x e y y el coeficiente de correlación múltiple entre y, y las x_i (a sus cuadrados se les llama coeficiente de determinación)