DISCRIMINACION
COMO DESCRIPCION
-ANALISIS FACTORIAL-DISCRIMINANTE-
Como ya hemos señalado, en muchas ocasiones, nos interesan mucho más los aspectos descriptivos del análisis discriminante que las reglas de decisión o de asignación. Esto ocurre cuando, en esencia, estamos fundamentalmente interesados en obtener procedimientos para averiguar el poder discriminante de las variables sobre grupos de individuos ya dados: Deseamos determinar su capacidad de discriminación, reducir, en la medida de lo posible su número, e incluso, ser capaces de obtener funciones de ellas, factores discriminantes, capaces de mejorar la "correcta" clasificación. Por último, obtenidos estos factores, podemos "reclasificar" los individuos y comprobar si nuestro análisis anterior era o no válido.
Todos estos objetivos los cumple a la perfección el análisis factorial discriminante.
Así pues, los objetivos que perseguimos con el análisis factorial discriminante son básicamente:
Seleccionar qué variables resultan más discriminantes de entre las disponibles.
Obtener los llamados factores o funciones discriminantes, que no son otra cosa que nuevas variables que serán combinaciones lineales de las variables discriminantes originales con un poder de discriminación óptimo.
Interpretar los factores discriminantes; lo que podrá hacerse a partir de las correlaciones de éstos con las variables originales, análogamente a como interpretábamos la estructura factorial en el Análisis Factorial. Aquí se trata, obviamente, de interpretar la estructura de diferenciación o estructura discriminante.
Ser capaces, por último, de clasificar a los individuos en base a los factores discriminantes obtenidos.
Como señala Lachenbruch el análisis factorial discriminante puede verse como un conjunto de técnicas para la descripción y el contraste de las diferencias entre grupos reproduciendo muchos de los criterios y técnicas del análisis multivariante de la varianza (MANOVA).
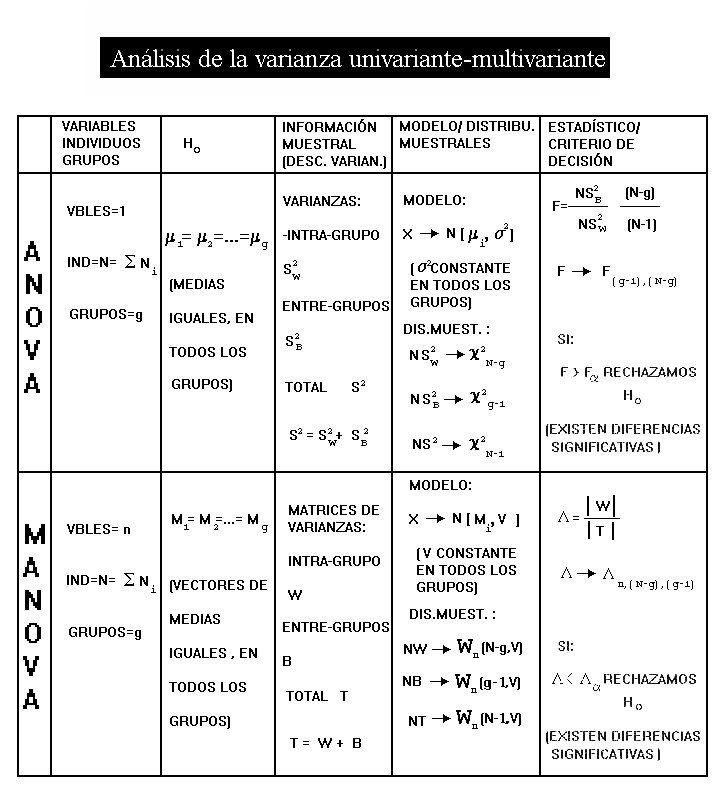
ANALISIS MULTIVARIANTE DE LA VARIANZA (MANOVA)
Si el análisis de la varianza univariante pretende contrastar hipótesis lineales sobre la influencia de los distintos niveles de uno o varios factores en el comportamiento de una variable (unidimensional), el análisis multivariante de la varianza (MANOVA) tiene la misma pretensión, pero considerando un vector (multidimensional) de variables.
La aplicación paradigmática del análisis de la varianza es determinar si existen diferencias significativas entre los distintos niveles o grupos de un factor ( categórico), a través del contraste de igualdad de medias. Porque es, fundamentalmente, ésta la aplicación que nos interesa, aquí nos detendremos un poco en ella, para el caso multivariante del MANOVA, para luego poder extender sus resultados y consideraciones al análisis factorial discriminante.
Los supuestos del análisis serán los mismos en el caso del MANOVA que en el del análisis factorial discriminante y, en consecuencia, los mantendremos ya desde aquí:
Consideramos un vector aleatorio Y de dimensión n sobre el cuál obtenemos g muestras correspondientes a los g niveles, categorías o grupos considerados.
Suponemos que Y sigue, en cada una de las poblaciones de los g grupos una distribución Normal n-variante con vector de medias M (i= 1,2,...g),eventualmente distinto para cada grupo y matriz de covarianzas V, la misma para todas las poblaciones.
Bajo estos supuestos, consideraremos, también, que cada observación n-dimensional para cada grupo, i, puede expresarse de acuerdo con el siguiente modelo:
Yi = M + Ai + Ei
Donde: M es el vector de medias general. Ai es un vector n-dimensional que nos indica el efecto propio del nivel o grupo i-simo. Ei es un vector aleatorio que nos indica la desviación errática de las observaciones y se supone que sigue una distribución normal n-dimensional con vector de medias el vector nulo y matriz de varianzas V, la misma para todos los grupos (i=1,2,...g)
En estas circunstancias es fácil comprobar cómo el vector Yi tendrá, en cada grupo, i, una distribución:
Yi ® N [ (M + Ai ); V ]
Sobre este modelo nos plantemos contrastar la hipótesis nula de que todos los vectores A sean nulos:
H0: A1= A2=....= Ag =0
Esta hipótesis equivale a considerar que no hay diferencias en los vectores de medias de Y en cada uno de los grupos o que las medias en cada grupo son las mismas y coinciden el vector M .
Para la realización del contraste, partimos, como en el caso univariante, de la descomposición de la varianza total; en este caso de la matriz de varianzas y covarianzas total.
La matriz de varianzas muestrales T puede verse como la suma de otras dos matrices de varianzas: T = B + W
Donde B es la matriz de varianzas "entre-grupos" (Between-groups) y W es la matriz de varianza "intra- grupos" (Within-groups).
B expresa las varianzas y covarianzas, considerando los centroides de los grupos como observaciones.
W, en cambio, expresa la suma para todos los grupos de las varianzas y covarianzas de las observaciones de cada grupo.
Pues bien, la matriz NB, donde N es el número total de observaciones muestrales, puede probarse que sigue una distribución de Wishart con parámetros n, g-1 , V (lo que se expresa como Wn(g-1, V ) ).
La distribución puede considerarse como una generalización de la distribución c 2 de Pearson, que puede definirse de acuerdo con el siguiente esquema general:
Si tenemos una matriz de n columnas y m filas, Z; donde cada columna está formada por un vector aleatorio m-dimensional que tiene una distribución normal m-variante con vector de medias el vector nulo y matriz de varianzas V, la misma para todas las columnas de la matriz; entonces la matriz A = Z'Z sigue una distribución de Wishart de parámetros n, m y V [lo que puede expresarse como: Wn (m,V) ]
Una propiedad importante de esta distribución es que si realizamos un muestreo aleatorio de tamaño N sobre una población normal multivariante N [M,V],la matriz formada por el producto del escalar N y la matriz de varianzas muestral,S, sigue una distribución de Wishart de parámetros n, N-1, V: NS ® Wn (N-1, V )
Es, precisamente, a partir de esta propiedad como puede probarse el resultado de que :
NB ® Wn (g-1,V)
Igualmente puede probarse también que si la hipótesis nula: H0: A1= A2=....= Ag =0 es cierta, entonces la matriz NW seguirá, también una distribución de Wishart de parámetros n, N-g, V y será independiente de la distribución de NB.
Obviamente también, considerando esa misma propiedad, NS (siendo S la matriz de varianzas totales muestral ) seguirá también una distribución Wn (N-1,V)
Teniendo en cuenta ésto, el contraste de la hipótesis nula: H0: A1= A2=....= Ag =0 se lleva a cabo evaluando el valor del estadístico L (lambda de Wilks): L = |W| / |T|
Estadístico que sigue una distribución L de Wilks de parámetros n, N-g ,g-1 .
Es, precisamente este estadístico el que nos conducirá a determinar si los vectores de medias de los grupos son significativamente diferentes o no; es decir, si la hipótesis nula es rechazable o no:
Para un nivel de significación a:
Aceptaremos la hipótesis nula si L > La
Rechazaremos la hipótesis nula si L < La
Siendo L el valo crítico que verifica P (L > La) = a en una distribución L (n, N-g,g-1).
En la práctica el contraste se realiza después de una transformación previa del estadístico en una F o una c2

DETERMINACION DE LAS VARIABLES MAS DISCRIMINANTES
Como se ha comentado, uno de los objetivos de la discriminación descriptiva es determinar cuáles son , de entre las variables disponibles, aquellas que tienen un mayor poder
discriminativo. Es evidente que este objetivo es tanto más importante si el número de variable de las que se dispone información es muy elevado o si este número excede al número máximo de variables que pueden utilizarse en una factorización posterior.
Determinar qué variable es más discriminante y las que tienen, sucesivamente, mayor poder discriminativo puede hacerse a partir de un análisis de la varianza (univariante) para cada variable; obteniendo que una variable es tanto más discriminativa cuanto mayor sea su estadístico F.
Si queremos determinar qué grupos de variables de un determinado tamaño es el más discriminativo, podemos considerar todos los posibles grupos de ese tamaño y realizar un análisis MANOVA , decantándonos por el grupo de variables que presente un menor valor de su estadístico L de Wilks.
Procediendo de esta manera, podemos, desgraciadamente, acabar seleccionando un conjunto de variables que resulten estar altamente correlacionadas entre sí, proporcionándonos, en consecuencia, una discriminación redundante. Para evitar este problema, los distintos algoritmos de discriminación "paso-a-paso " utilizan "criterios de tolerancia" para la selección de las variables como variables discriminantes
De todas manera, la determinación del conjunto de variables a considerar como variables discriminantes es, en la práctica, algo que se realiza a la vez que la determinación de los factores o ejes discriminantes utilizando los ya mencionados procedimientos paso a paso.
Especialmente nos centraremos en el procedimiento de selección y discriminación basado en la mínimización del estadístico L de Wilks, que es el que utilizaremos en nuestro estudio.
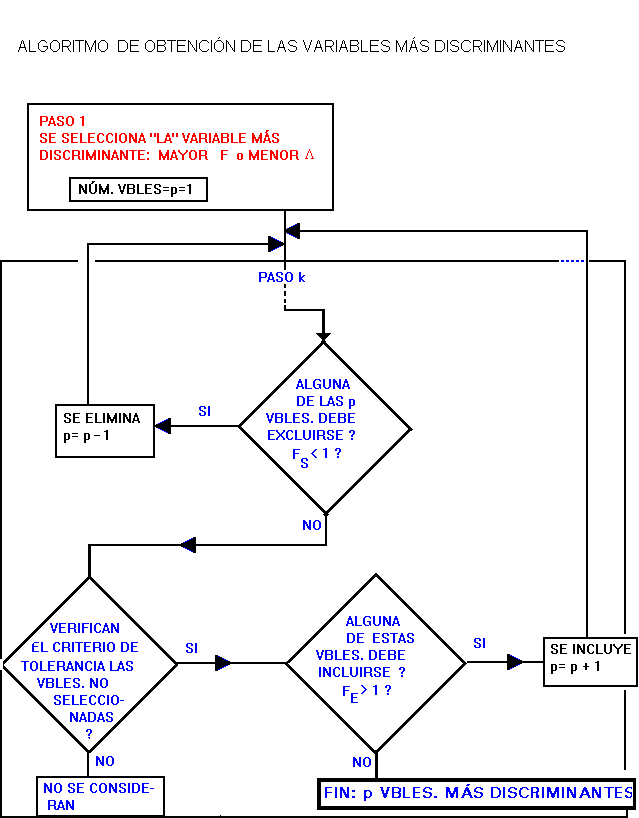
Siendo los criterios de selección habituales ( en el algoritmo de Wilks):

Una vez obtenidas el conjunto de variables más discriminantes, la solución puede mejorarse obteniendo un conjunto alternativo de nuevas variables discriminantes, llamadas factores o funciones discriminantes, capaces de discriminar de una forma más contundente y que se obtienen como combinación lineal de la solución obtenida. En el siguiente gráfico se pone de manifiesto, lo que queremos decir:
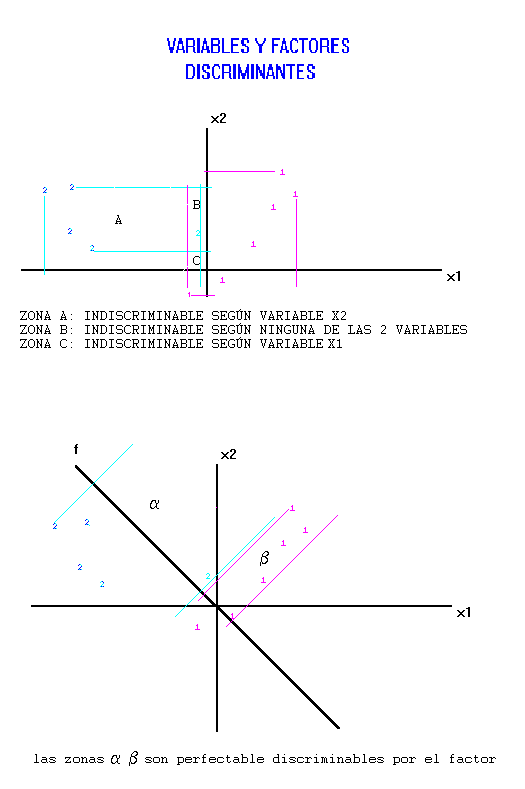
Para obtener estos factore o funciones discriminantes se opera de acuerdo al siguiente esquema:

Y finalmente podemos utilizar los resultados del análisis para la clasificación ( o reclasificación) de los individuos:
