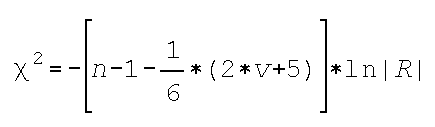
|
|
|
|
EXAMEN DE LA MATRIZ DE CORRELACIONES
El primer paso en el Análisis Factorial será calcular la matriz de correlaciones entre todas las variables que entran en el análisis.
|
Matriz de
correlaciones del análisis socio-demográfico del A.M.V. |
Una vez que se dispone de esta matriz concierne examinarla para comprobar si sus características son adecuadas para realizar un Análisis Factorial. Uno de los requisitos que deben cumplirse para que el Análisis Factorial tenga sentido es que las variables estén altamente correlacionadas.
Pueden utilizarse diferentes métodos para comprobar el grado de asociación entre las variables:
El determinante de la matriz de correlaciones: un determinante muy bajo indicará altas intercorrelaciones entre las variables, pero no debe ser cero (matriz no singular), pues esto indicaría que algunas de las variables son linealmente dependientes y no se podrían realizar ciertos cálculos necesarios en el Análisis Factorial).
Test de Esfericidad de
Bartlett: Comprueba que la
matriz de correlaciones se ajuste a la matriz identidad ( I), es decir
ausencia de correlación significativa entre las variables. Esto significa que la
nube de puntes se ajustara a una esfera perfecta, expresando así la hipótesis
nula por:
Ho: R = I
es decir, que el determinante de la matriz de correlaciones es 1.
Ho: | R| = 1
La formula correspondiente asume la siguiente expresión:
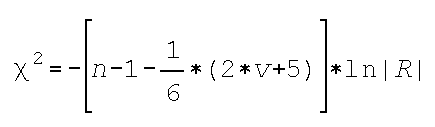
donde...
n =tamaño muestral.
v =número de variables.
ln=logaritmo neperiano.
R =matriz de correlaciones.
si se acepta la hipótesis nula (p>0.05) significa que las variables no están intercorrelacionadas y por tanto no tiene mucho sentido llevar a cabo un Análisis Factorial.
Es muy útil cuando el tamaño muestral es pequeño.
- Indice KMO de Kaiser-Meyer-Olkin:
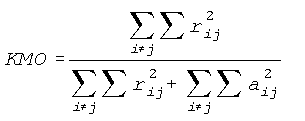
donde...
rij= correlación simple.
aij= correlación parcial.
Valores bajos del indice KMO desaconsejan la utilización de Análisis Factorial.
Como baremo para interpretar el índice KMO podría tomarse según Kaiser:
1 >= KMO >= 0.9 muy bueno
0.9 >= KMO >= 0.8 meritorio
0.8 >= KMO >= 0.7 mediano
0.7 >= KMO >= 0.6 mediocre
0.6 >= KMO > 0.5 bajo
KMO <= 0.5 inaceptable
- Correlación Anti-imagen: que es el negativo del coeficiente de correlación parcial, deberá haber pocos coeficientes altos para que sea razonable aplicar el Análisis Factorial.
- Medida de Adecuación de la
Muestra (MSA):

donde...
rij= correlación simple.
aij= correlación parcial.
valores bajos de este índice desaconsejan el uso del Análisis Factorial.
- Correlación Múltiple, que deberá ser alto, sobre todo si la técnica a utilizar es un análisis factorial. Esta técnica, por defecto, toma los valores de la correlación múltiple al cuadrado como los valores iniciales de comunalidad.
Ir a Análisis factorial para estructura socio-demográfica del AMV
Ir a Análisis factorial para estructura económica del AMV
Ir a fase factorial del análisis estructural

