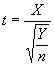DISTRIBUCIÓN t DE STUDENT

ir a distribuciones derivadas de la normal

La distribución t de student (desarrollada por Gosset ) es , con la chi2 , la F de Snedecor, y , por supuesto, la normal , transcendental para aplicaciones inferenciales , en especial para aquellas en las que se desconoce la varianza ; dado que no depende de las varianzas de las variables que la integran.

Su expresión formal parte de dos variables X e Y tales que :

      e        de manera que 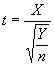                        siendo t una nueva distribución conocida como t de student con n grados de libertad.

La distribución t de student . admite , tambien , una definición alternativa , tomada como la distribución marginal de la primera variable de una distribución "normal-gamma" ; en este sentido la expresión de su función de densidad vendría dada por :

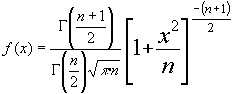                                             siendo n los grados de libertad que actuan de parámetro    y     la función gamma de Euler

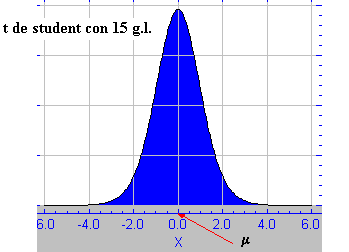
La distribución t de student con n grados de libertad tiene siempre como media el valor "0" , sea cuales fueren los grados de libertad ; es simétrica ,asitóticamente tiende a ,de forma campaniforme , al igual que la distribución normal, teniendo como varianza el valor

Los valores de la función de probabilidad para los diversos están tabulados atendiando al único parámetro de la distribución , es decir , el número de grados de libertad ; evidentemente , es más recomendable para su cálculo la utilización del programa que presentamos.

En otro orden de cosas la distribucción t de student con n grados de libertad congerge en ley a una normal tipificada (estandarizada ) cuando el número de grados de libertad tiende a infinito