Si, a partir de una variable X que siga una distribución Normal obtenemos una variable z que sea :

            su función de densidad vendrá  dada por la siguiente expresión :

                             donde             dado que         :

                               así                    

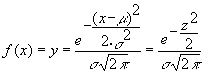
                       luego                   

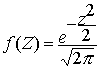
Comparando ¦ (z) con ¦ (x) es fácil ver que la función de densidad de z sería la de una distribución normal que tenga por parámetros m = 0 y s = 1

A partir de este resultado y aplicando las características ya estudiadas de la función de una normal , se puede concluir las siguientes propiedades de la "distribución-normal-cero-uno":

Su función de densidad es simétrica respecto z = 0

Su función de densidad presenta dos asíntotas para tendiendo a cero por ambos lados

Presenta dos puntos de inflexión en z = ± 1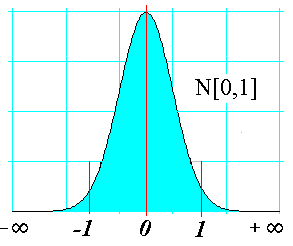

Presenta un máximo en z=0  . Así  su representación gráfica sería: