1. Introducción
2. La distribución Normal general
3. La distribución Normal Reducida
(Tipificada)
3.1.Comprobación de que la distribución
Normal Reducida es una distribución de probabilidad
4. Funciones de distribución .
ejemplo 1
5. Función generatriz de momentos
6. Media y Varianza de la Distribución
Normal .
7. Coeficientes de asimetría y kurtosis de
la distribución normal .
8. Teorema de adición
.
ejemplo 2
9. Teorema Fundamental de las
Distribuciones Normales
. ejemplo 3
10. Distribuciones
Normales-Transformadas
La distribución normal es , con mucho , la más importante de todas las distribuciones de probabilidad . Es una distribución de variable continua ,con campo de variación ]-¥ ,¥ [ . Fue ‚ descubierta por Gauss al estudiar la distribución de los errores en las observaciones astronómicas.
Debe su importancia a tres razones fundamentales:
Por un lado, un gran número de fenómenos reales se pueden modelizar con esta distribución (tales el caso de las características cuantitativas de casi todas las grandes poblaciones), por otro lado, muchas de las distribuciones de uso frecuente tienden a aproximarse a la distribución normal bajo ciertas condiciones ; y , por último ,en virtud del Teorema Central del Límite, todas aquellas variables que puedan considerarse causadas por un gran número de pequeños efectos (como pueden ser los errores de observación) tienden a distribuirse con una distribución normal.
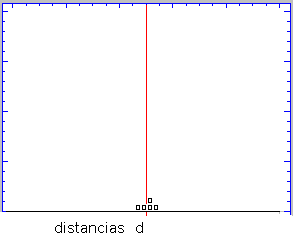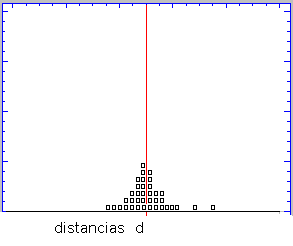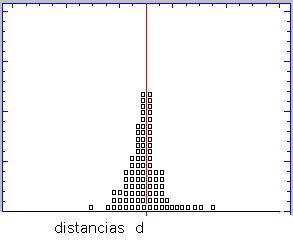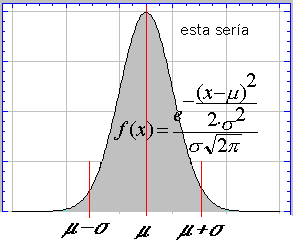 Para
comprender mejor la distribución normal planteemos su descubrimiento , en un
pequeño gráfico animado. Nos encontramos midiendo la distancia a un astro (d) ;
evidentemente cada distancia observada no ha de ser es igual a la anteriormente
tomada pues cometemos errores medición , bien por nosotros , bien por lo
instrumentos . Teóricamente un error puede ser tan grande que la distancia observada sea
mas infinito, y también teóricamente , menos infinito. Plasmamos en un gráfico, y
sobre un eje , cada observación que realizamos ( en el gráfico un cuadrado). Cuantas
más observaciones realizamos los diversos cuadrados , en conjunto , van
tomando una determinada forma ; si nos planteamos calcular la expresión analitica
de dicha forma llegamos a la función de la curva , que tomada como función de
densidad , pues posee las características de dicho tipo de funciones , es la de la
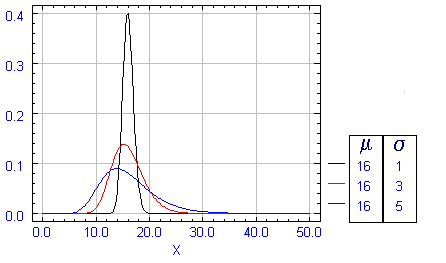
distribución normal . Dependiente , como se observa de dos párametros : uno , el valor
central de la curva , y ,otro, la distancia de dicho valor a los puntos de inflexión
(luego comprobaremos que dichos parámetros son la media y la desviación típica)
Para
comprender mejor la distribución normal planteemos su descubrimiento , en un
pequeño gráfico animado. Nos encontramos midiendo la distancia a un astro (d) ;
evidentemente cada distancia observada no ha de ser es igual a la anteriormente
tomada pues cometemos errores medición , bien por nosotros , bien por lo
instrumentos . Teóricamente un error puede ser tan grande que la distancia observada sea
mas infinito, y también teóricamente , menos infinito. Plasmamos en un gráfico, y
sobre un eje , cada observación que realizamos ( en el gráfico un cuadrado). Cuantas
más observaciones realizamos los diversos cuadrados , en conjunto , van
tomando una determinada forma ; si nos planteamos calcular la expresión analitica
de dicha forma llegamos a la función de la curva , que tomada como función de
densidad , pues posee las características de dicho tipo de funciones , es la de la
distribución normal . Dependiente , como se observa de dos párametros : uno , el valor
central de la curva , y ,otro, la distancia de dicho valor a los puntos de inflexión
(luego comprobaremos que dichos parámetros son la media y la desviación típica)
La distribución normal es una distribución de variable continua que queda especificada por dos parámetros de los que depende su función de densidad y que resultan ser la media y la desviación típica de la distribución . Su estudio teórico suele introducirse directamente a partir de su función de densidad.
2. La distribución Normal general
Como se ha dicho ,depende de dos parámetros , m , s , que como luego comprobaremos , son su media y su desviación típica .
El hecho de que una variable x se distribuya con una distribución normal de media m y desviación típica s se representa por:
X ® N[m
;s ] ó L(X)®
N[m ;s ]
(Aunque nosotros seguiremos este sistema de especificación , es bastante corriente ,
también ‚ que a la distribución normal se la especifique por los parámetros media
y varianza ( en vez de desviación típica), m , s 2
Su función de densidad es:
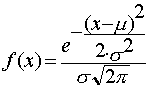
![]()
Las características de dicha función de densidad serán:
Si realizamos la primera derivada de dicha función tendremos que :
dado que : 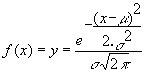
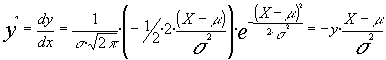
la segunda derivada será: 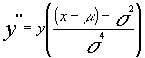
Igualando a cero la primera derivada obtenemos que y'=0 para X = m y para X = ¥ .
Como la segunda derivada en x = m es negativa ,concluimos que la función de densidad presenta un máximo en X = m , lo que nos hace afirmar que la media ( m ) es también la moda de la distribución normal.
Es fácil comprobar que la función de densidad presenta dos puntos de
inflexión en los valores X = ![]()
Por otro lado para cualquier valor de a se verifica que: ¦ (m +a)= ¦ (m -a) por lo que la función es simétrica respecto a m
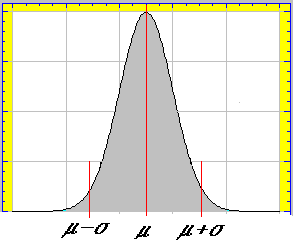
Teniendo en cuenta estos resultados la representación gráfica de la función de densidad resultaría de la siguiente manera:
3. La distribución Normal Reducida (Tipificada)
Si,
a partir de una variable X que siga una distribución Normal obtenemos una variable z que
sea : ![]()
su función de densidad vendrá dada por la siguiente expresión :
![]() donde
donde
![]() dado que
:
dado que
: ![]()
![]()
así
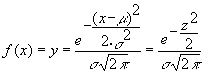
luego
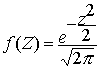
Comparando ¦ (z) con ¦ (x) es fácil ver que la función de densidad de z sería la de una distribución normal que tenga por parámetros m = 0 y s = 1
A partir de este resultado y aplicando las características ya estudiadas de la función de una normal , se puede concluir las siguientes propiedades de la "distribución-normal-cero-uno":
Su función de densidad es simétrica respecto z = 0
Su función de densidad presenta dos
asíntotas para ![]() tendiendo a cero por ambos lados
tendiendo a cero por ambos lados
Presenta dos puntos de inflexión en z = ±
1 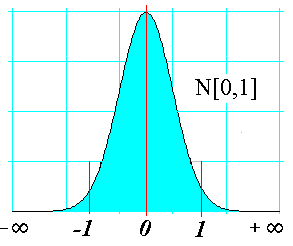
Presenta un máximo en z=0 . Así su representación gráfica sería:
3.1.Comprobación de que la distribución Normal Reducida es una distribución de probabilidad
La función de densidad es siempre positiva por lo que bastará para probar que puede ser una distribución de probabilidad con el hecho de comprobar que su función de distribución toma el valor 1 en el infinito: es decir F(¥ )=1
Así
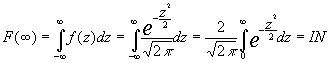
Conocemos por otra parte que la integral
impropia (integral de Poisson) es 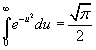
siendo ,evidentemente , U una función de z.
por lo que realizando
el cambio ![]() por lo que
por lo que ![]() y
y ![]()
tendremos que la integral que buscamos resolver será:
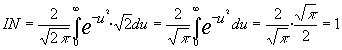
por lo que se demuestra que es función de distribución de probabilidad.
Como ya conocemos la distribución normal(general) de probabilidad tiene una función de densidad
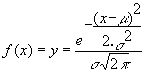
que integrada para todo su campo ]-¥ ,¥ [ daría como resultado la expresión analítica de su función de distribución de probabilidad . Para el cálculo de probabilidades especificas para un determinado valor de la variable X ( que se plantea que se distribuye según una Normal) tendríamos que la probabilidad de que la variable X se menor o igual (el hecho igual es indiferente pues estamos ante una variable continua) a un valor X1 es :
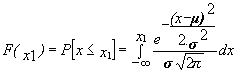
La realización de este cálculo de probabilidad supone la realización de la integral y dependerá para cada caso del valor de los parámetros de la función m y s .
Dado que los valores que pueden tener dichos parámetros son infinitos y distintos para cada caso , nos vemos en la necesidad de realizar la integral y el cálculo para cada valor de probabilidad que queramos establecer. Para solventar este problema operativo la solución radica en transformar la normal con la que estemos trabajando en la normal tipificada N[0;1] . ; tipificando los valores de la variable de los que queramos establecer probabilidades.
De esta manera solo tendremos que actuar con la función de densidad de la normal reducida que , evidentemente , es más sencilla de manera que:
si X® N[m ; s ] y
pretendemos ,como en párrafo anterior, calcular ![]()
haríamos : trabajar, con la más sencilla , normal reducida Z® N[0;1]
calculando ![]() donde
donde ![]() es decir el valor
tipificado de X1
es decir el valor
tipificado de X1
de esta manera tendríamos que
realizar: 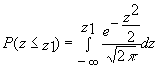 que resulta más fácil de resolver
que resulta más fácil de resolver
dado que todas las distintas normales con las que nos podemos encontrar son susceptibles de transformarse en "tipificadas" , la única que tiene sus valores tabulados en una tabla es , precisamente, la normal [ 0;1] . Si bien lo anteriormente mencionado ha sido lo habitual , en estos momentos, y gracias a las posibilidades informáticas, es posible establecer algoritmos de ejecución para cualquier par de parámetros que definan una normal , y es posible por ello el cálculo de probabilidades "directo" sin necesidad de tipificar los valores de la variable. Este tipo de algoritmo funciona , como se puede comprobar, en el "script" de la distribución normal que presentamos.( ir a script de la normal)
Sea X una variable aleatoria que se distribuye según una normal de media 5 y desviación típica 2 . Calcular la probabilidad de que dicha variable tome valores inferiores a 4 .
X® N(5;2) se nos
pide ![]() sin utilizar tablas
o algoritmos de recurrencia tendríamos que realizar la integral :
sin utilizar tablas
o algoritmos de recurrencia tendríamos que realizar la integral :
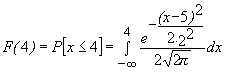
para no tener que resolver dicha integral y dado que no podemos tener tabuladas todas las posibles distribuciones normales ( por ejemplo esta , la N(5;2)) transformaremos el valor de la variable sobre el que queremos calcular una probabilidad aun valor tipificado (estandarizado) , para poder usar la tabla de la N(0;1) que habitualmente tenemos a mano realizada-calculada por varios autores . Así , siendo t® N(0;1) tendríamos:
![]()
así el efecto de lo apuntado sería el expuesto en la imagen:

Utilizando una tabla de la normal 0,1 obtendríamos el valor 0.691
Si utilizamos el script para el cálculo de probabilidades en la distribución normal que presentamos , no es necesaria la tipificación ,y el cálculo es directo. (ir a script de la normal)
5. Función generatriz de momentos
Vamos a calcular primero la F.G.M. de la distribución normal reducida
v(t). Una vez obtenida ‚ esta , teniendo en cuenta que una variable normal general
puede verse como una transformación lineal de una variable normal reducida
[ x=s z +m ]
,obtener la F.G.M. de la normal general ser sencillo ya que:
![]()
siendo la F.G.M. de la normal reducida
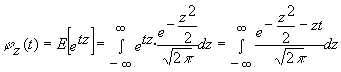
manipulando el exponente tendremos que:
![]()
![]()
con lo que la F.G.M. quedar :
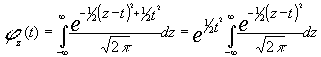
si llevamos a cabo el cambio de variable u=z-t tendremos que :
dz = du y además si : ![]() y si
y si
![]()
tendremos que : 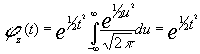
ya que el integrando ,prescindiendo del nombre de la variable es la función de densidad de una normal reducida que integrada para todo el campo da uno.
Así pues la F.G.M. de la normal reducida es:
![]()
![]()
![]()
Y, por tanto , la F.G.M. de la normal general
será : ![]()
6. Media y Varianza de la Distribución Normal
La media es el momento ordinario de primer
orden ( E(x)= ![]() ) y, por lo tanto será (según el teorema que conocemos como de
los momentos) el valor que tome la primera derivada de la función generatriz en el
punto t =0.
) y, por lo tanto será (según el teorema que conocemos como de
los momentos) el valor que tome la primera derivada de la función generatriz en el
punto t =0.
luego aplicando lo enunciado:
![]() que para el valor de t
= 0
que para el valor de t
= 0
tomará el valor ![]() con lo que queda demostrado
con lo que queda demostrado
que la media de la distribución normal es su parámetro m
La varianza , como conocemos, es ![]() siendo
siendo ![]() el momento ordinario de orden
segundo ;
el momento ordinario de orden
segundo ;
que obtendremos aplicando el valor t = 0 a la segunda derivada de la Función
Generatriz de Momentos. Así:
![]()
![]() que
para el valor t = 0 será:
que
para el valor t = 0 será:
![]()
por
lo que la varianza quedará : ![]()
lo que nos indica que
la varianza de la distribución normal coincide con su parámetro s
al cuadrado ;
lógicamente la desviación típica será
s .
7. Coeficientes de asimetría y kurtosis de la distribución normal
Dado que se trata de calcular el coeficiente de asimetría para cualquier distribución normal , pues es evidente que todas tendrán la misma forma . Es conveniente que nos planteemos la resolución para la normal reducida N[0;1] , lo que lógicamente nos ahorrará cálculos
El coeficiente de asimetría de la normal
reducida o tipificada ,![]() , es el momento central de tercer orden de dicha variable tipificada
(z), así:
, es el momento central de tercer orden de dicha variable tipificada
(z), así:![]()
![]()
ya que la media de la variable tipificada es cero , para calcular el coeficiente de asimetría nos bastará con calcular el momento ordinario de tercer orden de la variable tipificada. y el momento de tercer orden de la variable tipificada será el valor que tome la tercera derivada de la F.G.M. de la distribución de z ( normal reducida) en el punto t =0:
la F.G.M de la tipificada resultaba ser ![]()
la primera derivada
será ![]()
luego para t = 0 será ![]()
la segunda derivada será
![]()
luego para t = 0 ![]()
la tercera derivada
será ![]() o lo que es lo mismo
o lo que es lo mismo
![]()
haciendo t =0 tendremos que :
![]()
luego quedaría ![]()
Por lo que el coeficiente de asimetría de la distribución normal es cero lo que supone , como cabría esperar, que la distribución es simétrica.Su eje de simetria es la media ( µ ) que por esta razón es también le mediana de la distribución
En cuanto al coeficiente de kurtosis , operaremos de la misma manera que lo hicimos con el de asimetría, es decir ,basándonos en la normal reducida .Conocemos que dicho coeficiente es el momento central de cuarto orden de la variable tipificada menos tres unidades . Pero al tratarse de una variable tipificada , cuya media es cero el momento central debe coincidir , y coincide con el momento ordinario ; es decir , con el valor de la cuarta derivada de la Función Generatriz de Momentos para el valor t = 0.
tendremos así que la cuarta derivada de
F.G.M. es : ![]()
![]()
![]() para
t = 0 tendremos que :
para
t = 0 tendremos que :
![]() por tanto el
valor del momento central de orden cuarto toma el valor 3.
por tanto el
valor del momento central de orden cuarto toma el valor 3.
así , planteando el coeficiente de kurtosis
como ![]() el coeficiente de
Kurtosis es 0 ; como se puede constatar el hecho de que haya resultado 0 , es precisamente
por habérsele restado el propio valor del momento central de orden cuarto , para con ello
tomar la forma de la distribución normal como modelo de comportamiento para otras
distribuciones , de ahí que algunos autores consideren que el coeficiente de Kurtosis no
tiene como valor de referencia centrado el 0 , si no el 3 . Es por tanto la distribución
normal la que posee la forma tipo en cuanto a aplastamiento o apuntamiento , y sirve de
modelo para las demás distribuciones.
el coeficiente de
Kurtosis es 0 ; como se puede constatar el hecho de que haya resultado 0 , es precisamente
por habérsele restado el propio valor del momento central de orden cuarto , para con ello
tomar la forma de la distribución normal como modelo de comportamiento para otras
distribuciones , de ahí que algunos autores consideren que el coeficiente de Kurtosis no
tiene como valor de referencia centrado el 0 , si no el 3 . Es por tanto la distribución
normal la que posee la forma tipo en cuanto a aplastamiento o apuntamiento , y sirve de
modelo para las demás distribuciones.
La distribución normal verifica el teorema de adición para los parámetros media y varianza . Esto es, dado un conjunto de variables aleatorias normales independientes de distintas medias y distintas varianzas , la variable suma de todas ellas se distribuirá según una distribución normal con media, la suma de las medias; y con varianza , la suma de las varianzas.
Teniendo en cuenta que nosotros hemos caracterizado la distribución normal con los par metros media , m , y desviación típica , s , el enunciado del teorema quedaría de la siguiente manera:
Dado un conjunto de variables aleatorias normales independientes de distintas medias y distintas desviaciones típicas , la variable aleatoria suma de todas ellas se distribuir según una distribución normal , con media , la suma de las medias ; y con desviación típica , la raíz cuadrada de la suma de los cuadrados de las desviaciones típicas.
Teniendo en cuenta la recursividad de la operación suma, para demostrar el teorema para cualquier número de variables aleatorias basta probarlo para el caso de dos variables.
Demostración:
Sean X e Y dos variables aleatorias independientes y tales que:
X® N [m x ; s x ]
Y® N [m y ; s y ]
queremos comprobar que la variable U=X +Y es tal que:
![]()
Así y en efecto:
por ser x e y normales sus Funciones Generatrices de Momentos serán:
para X será ![]()
para Y será ![]()
dado que son independientes , la F.G.M . de la suma será el producto de las Funciones Generatrices de Momentos
y así: ![]()
luego :![]() que es la
función generatriz de momentos de una distribución normal con media
que es la
función generatriz de momentos de una distribución normal con media ![]() y varianza
y varianza ![]()
luego lo es de la distribución : ![]()
queda , por tanto , demostrado que la distribución normal verifica el teorema de adición para los parámetros : m y s
Dos variables X e Y son independientes y ,
además se distribuyen normalmente de manera que: X® N(2;1)
mientras que Y® N(4;2) ; suponemos que Z=X+Y . Nos preguntamos
por cuál será la distribución y parámetros de la variable Z.
dado que X e Y son normales e independientes la variable Z también será normal y en aplicación del teorema de adición tendremos que sus parámetros serán:
![]()
![]() por lo que Z® N(6 ; 2,236)
por lo que Z® N(6 ; 2,236)
9. Teorema Fundamental de las Distribuciones Normales
Se trata de una generalización del teorema anterior: "cualquier combinación lineal de variables aleatorias normales independientes es una variable aleatoria normal con media la misma combinación lineal de las medias y con varianza la combinación lineal de las varianzas con los coeficientes que las acompañan al cuadrado ".(Su desviación típica será la raíz cuadrada de esta combinación lineal)
Sean las variables aleatorias Xi , con i=1,2,3,...n, todas ellas independientes tales que:
![]() y sean los
números reales a i con i=1,2,3,...n
y sean los
números reales a i con i=1,2,3,...n
la
variable combinación lineal : ![]()
se distribuirá según : 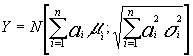
Demostración: a partir de cada variable Xi construimos la correspondiente variable , ui = ai xi
por ser las u transformaciones lineales de las xi sus F.G.M. serán:
![]()
las nuevas variables ui
son también ‚ independientes y , por otro lado , la variable Y se puede descomponer
como la suma de las variables ui . y así
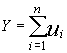
de forma que la F.G.M. de la variable Y será el producto de las F.G.M. de las ui , por ser‚ estas independientes:
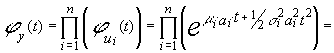
![]()
cuya expresión no es más que la Función Generatriz de Momentos de
una distribución normal
con media 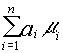 y varianza
y varianza 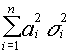 tal y como
queríamos demostrar
tal y como
queríamos demostrar
Una pieza J está compuesta por 2 elementos de A y uno de B , que se unen sin solapamiento . La longitud de las piezas A sigue una N[4;1] cm. , mientras que las B también son normales N[12;2]cm. . Queremos conocer la probabilidad de crear una pieza J de longitud inferior a 20,2 cm
Longitud de J = longitud de A+ longitud de A + longitud de B
y no Longitud de J = 2veces longitud de A + longitud de B
dado que si una pieza A es de una determinada longitud aleatoria la otra pieza A no tiene porque ser de la misma longitud (aunque proceda o se distribuya con la misma distribución de probabilidad). A parte de esto ,el hecho de utilizar suma o producto no da el mismo resultado al aplicar el teorema fundamental de las distribuciones normales , dado que la suma o producto se realizan dentro de una raíz . Por ello ,en este caso , hemos de tomar la primera expresión , así:
L(J)=L(A)+L(A)+L(B) simplificando J=A+A+B dado que:
A® N [ 4; 1] y B® N[12; 2] y son independientes:
y en aplicación del teorema fundamental de las distribuciones normales , tendremos que
![]()
Luego J® N[20 ; 2.449]
y que evidentemente no resultaría lo mismo si hubiésemos hecho, como antes dijimos, :
![]()
Conociendo que la verdadera longitud de la pieza es J® N[20 ; 2.449]
se nos pregunta por : ![]()
siendo el resultado según tabla de la N[0;1] ; 0.532
Resultado que sería el mismo de haber aplicado directamente el "script" de la distribución normal (ir a script de la normal)
10. Distribuciones Normales-Transformadas
Una variable aleatoria x sigue una distribución normal-transformada si, no siendo ella misma normal, si lo es una cierta función de ella:
z = h (x) ® N [m ;s ]
la función de densidad de x será :
![]() donde el jacobiano
donde el jacobiano ![]()
de forma que la función de densidad quedaría de la siguiente manera :
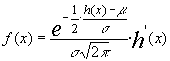
Un caso especialmente importante es el de la distribución logaritmo-normal , log-normal, o distribución de Galton:
X sigue una distribución de Galton si Z = ln (x - a) ® N (m ; s )
y ,
así , su función de densidad será : 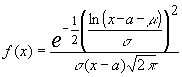
que evidentemente , sólo estará definida para valores x > a.
a modo orientativo planteamos la forma de tres distribuciones lognormales con medias y varianza distintas :