Vamos a calcular primero la F.G.M. de la distribución normal reducida v(t). Una vez obtenida ‚ esta , teniendo en cuenta que una variable normal general puede verse como una transformación lineal de una variable normal reducida
[ x=s z +m ] ,obtener la F.G.M. de la normal general ser  sencillo ya que:

                                                              siendo la F.G.M. de la normal reducida           

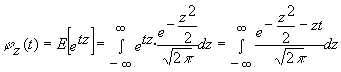
                                                        manipulando el exponente tendremos que:

                                                                con lo que la F.G.M. quedar :

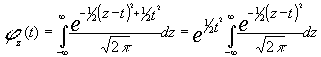
                        si llevamos a cabo el cambio de variable u=z-t tendremos que :

                       dz = du    y además si :       y   si     

                tendremos que :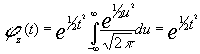        

ya que el integrando ,prescindiendo del nombre de la variable es la función de densidad de una normal reducida que integrada para todo el campo da uno.

Así pues la F.G.M. de la normal reducida es:           

Y, por tanto , la F.G.M. de la normal general será :