Se trata de una generalización del teorema anterior: "cualquier combinación lineal de variables aleatorias normales independientes es una variable aleatoria normal con media la misma combinación lineal de las medias y con varianza la combinación lineal de las varianzas con los coeficientes que las acompañan al cuadrado ".(Su desviación típica será la raíz cuadrada de esta combinación lineal)

Sean las variables aleatorias X_i , con i=1,2,3,...n, todas ellas independientes tales que:

                          y sean los números reales a _i con i=1,2,3,...n

       la variable combinación lineal :      

            se distribuirá según :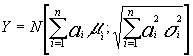

Demostración: a partir de cada variable X_i construimos la correspondiente variable  ,   u_i = a_i x_i

por ser las u transformaciones lineales de las x_i sus F.G.M. serán:

las nuevas variables u_i son también ‚ independientes y , por otro lado , la variable Y se puede descomponer como la suma de las variables u_i .   y así    

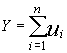
    de forma que la F.G.M. de la variable Y será  el producto de las F.G.M. de las u_i , por ser‚ estas independientes:

                                       
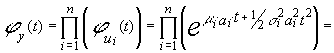
    cuya expresión no es más que la Función Generatriz de Momentos de una distribución normal

con media 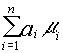     y varianza  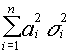     tal y como queríamos demostrar  (ejemplo)