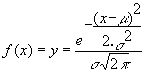
4. Funciones de distribución
Como ya conocemos la distribución normal(general) de probabilidad tiene una función de densidad
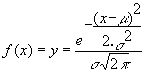
que integrada para todo su campo ]-¥ ,¥ [ daría como resultado la expresión analítica de su función de distribución de probabilidad . Para el cálculo de probabilidades especificas para un determinado valor de la variable X ( que se plantea que se distribuye según una Normal) tendríamos que la probabilidad de que la variable X se menor o igual (el hecho igual es indiferente pues estamos ante una variable continua) a un valor X1 es :
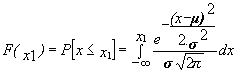
La realización de este cálculo de probabilidad supone la realización de la integral y dependerá para cada caso del valor de los parámetros de la función m y s .
Dado que los valores que pueden tener dichos parámetros son infinitos y distintos para cada caso , nos vemos en la necesidad de realizar la integral y el cálculo para cada valor de probabilidad que queramos establecer. Para solventar este problema operativo la solución radica en transformar la normal con la que estemos trabajando en la normal tipificada N[0;1] . ; tipificando los valores de la variable de los que queramos establecer probabilidades.
De esta manera solo tendremos que actuar con la función de densidad de la normal reducida que , evidentemente , es más sencilla de manera que:
si X® N[m ; s ] y
pretendemos ,como en párrafo anterior, calcular ![]()
haríamos : trabajar, con la más sencilla , normal reducida Z® N[0;1]
calculando ![]() donde
donde ![]() es decir el valor
tipificado de X1
es decir el valor
tipificado de X1
de esta manera tendríamos que
realizar: 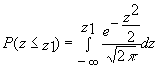 que resulta más fácil de resolver
que resulta más fácil de resolver
dado que todas las distintas normales con las que nos podemos encontrar son susceptibles de transformarse en "tipificadas" , la única que tiene sus valores tabulados en una tabla es , precisamente, la normal [ 0;1] . Si bien lo anteriormente mencionado ha sido lo habitual , en estos momentos, y gracias a las posibilidades informáticas, es posible establecer algoritmos de ejecución para cualquier par de parámetros que definan una normal , y es posible por ello el cálculo de probabilidades "directo" sin necesidad de tipificar los valores de la variable. Este tipo de algoritmo funciona , como se puede comprobar, en el "script" de la distribución normal que presentamos.( ir a script de la normal) (ejemplo 1)