|
|
|
|
REF.
I -2 Realizar el ejercicio anterior utilizando el test de Kolmogorov-Smirnov.
Así:
Se quiere comprobar si el número de asignaturas aprobadas en una determinada convocatoria universitaria sigue una distribución de Poisson (nivel de significación 0,05 ; para ello disponemos de la siguiente información de 60 alumnos :
| número de aprobadas | nº alumnos |
| 0 | 10 |
| 1 | 15 |
| 2 | 15 |
| 3 | 10 |
| 4 | 6 |
| 5 | 4 |
Tendremos que construir la tabla de frecuencias relativas acumuladas , tanto teóricas
como observadas : así
(ir a script de poisson)
| apr | n0,i |  |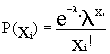
 |
 |
 |
| 0 | 10 | 0,1376 | 10/60=0,16 | 0,13 | 0,03 máximo |
| 1 | 15 | 0,272 | 25/60=0,41 | 0,4 | 0,01 |
| 2 | 15 | 0,270 | 40/60=0,66 | 0,67 | 0,01 |
| 3 | 10 | 0,1789 | 50/60=0,83 | 0,85 | 0,02 |
| 4 | 6 | 0,088 | 56/60=0,93 | 0,94 | 0.01 |
| 5 | 4 | 0,0351 | 1 | 0,98 | 0,02 |
el máximo resultado de la diferencia es 0,03 que será el estadístico a comparar en la tabla de K-S para un nivel de significación de 0.05 y n=60 tenemos que :
D0.05,60 = 
( ir a tabla de K-S) dado que es mayor que 0,03
no rechazamos la hipótesis de que los aprobados siguen una distribución de Poisson.
(ir a tets de K-S)
