de manera que cada una de ellas tenga una distribución 
donde
p=q=0,5 (Moivre introdujo la restricción p=q=0,5 , que no es necesaria tras la
generalización del teorema por Laplace)se establece que la nueva variable sucesión
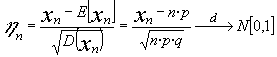
Teorema de Moivre (teoremas límite)
Es el primer teorema central del límite , históricamente hablando(1756).
Dada una sucesión de variables aleatorias {Xn}
de manera que cada una de ellas tenga una distribución donde
p=q=0,5 (Moivre introdujo la restricción p=q=0,5 , que no es necesaria tras la
generalización del teorema por Laplace)
se establece que la nueva variable sucesión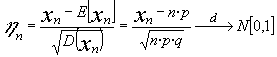
Lo demostraremos mediante la convergencia de la F.G.M.
Así la F.G.M de las variables de la sucesión (binomiales) Xn serán del tipo:
en consecuencia
la F.G.M. de la sucesión 
será :
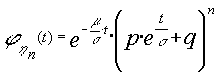
Pudiéndose probar que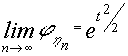 
que es la F.G.M. de la N[0,1]
Del teorema de Moivre-Laplace se deduce fácilmente que una
distribución binomial puede aproximarse a una distribución normal de media n·p y desviación típica 
cuando n tienda a infinito