La esperanza de la media muestral coincide con la media de la población, en definitiva ; la media de la media muestral es la media de la población :

en efecto :

                      así :

                  dado que para cualquier valor de i               ya que                pertenece a la población   ver complemento exel

             tendríamos que       

En cuanto a la varianza de la media muestral , tendremos que si el muestreo utilizado es aleatorio simple se cumple que                 en efecto :

dado que en el muestreo aleatorio simple las observaciones o elementos son independientes tendremos covarianzas iguales a cero y dado que :

para todo i

tendremos

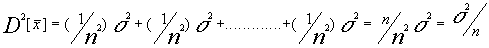
evidentemente la desviación típica será       

 en el caso de que el muestreo que hayamos realizado no sea aleatorio simple y que sea irrestricto y por tanto se plantee que no hay reemplazamiento siendo la población finita la media de la media muestral no sufrirá variaciones , pero no así la varianza de la media muestral que se verá afectada por el "coeficiente corrector de poblaciones finitas" (C .C .P.F. ), o "coeficiente de exhaustividad" , ya conocido del estudio de la distribución hipergeométrica. Así la varianza de la media muestral quedaría :

      siendo N el tamaño de la población (finita) y el resto lo habitual

Dado que ya conocemos la media y la varianza de la media muestral , y dado que podríamos tomar la muestra genérica como una sucesión de variables aleatorias independientes de media y varianza conocida , aunque con distribución desconocida , y en aplicación del T.C.L. , tendremos que la ley de la media muestral sea cual sea la distribución poblacional viene dada por :