Teorema Central del Límite ; Forma Lindeberg-Lévy
En cierto modo es un caso particular de la forma de Lyapounov pero con las premisas previas más restrictivas ; así
dada una sucesión de variables aleatorias {Xn}![]() independientes y con la misma distribución , de manera que las variables tendrán la
misma media y varianza :
independientes y con la misma distribución , de manera que las variables tendrán la
misma media y varianza : ![]() y
y ![]() tendremos que:
tendremos que:
La
sucesión ![]() definida como
:
definida como
: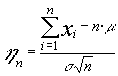
converge en distribución a una N[0,1]
de donde 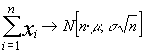 : es decir ;
: es decir ;
que si sumamos un gran número de variables aleatorias
independientes e igualmente distribuidas , con la misma media y varianza ; esta suma se
distribuirá normalmente con media n veces la media común y , desviación
típica raíz cuadrada de n veces la desviación típica común.
Para demostrar este teorema vamos aprobar que la F.G.M . de ![]() tiende a la F.G.M. de una distribución Normal reducida
cuando n tiende a infinito ; esto es :
tiende a la F.G.M. de una distribución Normal reducida
cuando n tiende a infinito ; esto es :
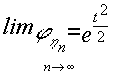 para ello consideramos las nuevas variables
tales que :
para ello consideramos las nuevas variables
tales que :
![]() para i = 1,2,3,......n .
de manera que :
para i = 1,2,3,......n .
de manera que :
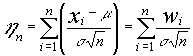 como todas las X son estocásticamente
independientes y están idénticamente distribuidas , las
como todas las X son estocásticamente
independientes y están idénticamente distribuidas , las ![]() también serán independientes y en consecuencia
tendrán la misma distribución ; así y en consecuencia la F.G.M. de
también serán independientes y en consecuencia
tendrán la misma distribución ; así y en consecuencia la F.G.M. de ![]() será:
será: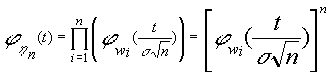 por lo que debemos obtener primero :
por lo que debemos obtener primero :
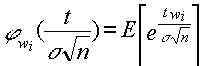
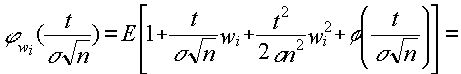
desarrollando en serie tendremos:
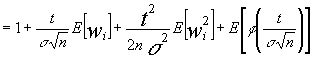 dado que :
dado que :
![]() y
y
![]() tendremos que
tendremos que
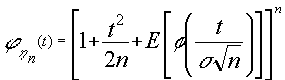
si
tomamos límites cuan n tiende a infinito la función ![]() es un infinitésimo de orden superior a
es un infinitésimo de orden superior a ![]() y por tanto :
y por tanto :
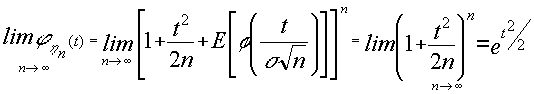
que es la expresión de la F.G.M. de la Normal (0;1).
Esta demostración es sólo valida para el caso en el que las F.G.M. existan ; si no fuera así utilizaríamos de manera análoga las funciones características.
Del propio teorema central del límite en forma Lindeberg-Lévy se
infiere , lo que podríamos denominar su versión en media ; así , dada una
sucesión de variables aleatorias {Xn}![]() independientes y con la misma
distribución de manera que las variables tendrán la misma media y varianza :
independientes y con la misma
distribución de manera que las variables tendrán la misma media y varianza : ![]() y
y ![]() y tenemos la sucesión :
y tenemos la sucesión :
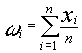 es decir, la media de la sucesión ; y dado que conocemos por
Lindeberg-Lévy que : La sucesión
es decir, la media de la sucesión ; y dado que conocemos por
Lindeberg-Lévy que : La sucesión ![]() definida como :
definida como :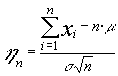 converge en distribución a una N[0,1] luego para la
nueva sucesión
converge en distribución a una N[0,1] luego para la
nueva sucesión ![]() tendremos que:
tendremos que:
la sucesión ![]() definida como :
definida como :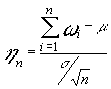 converge en distribución a
una N[0,1]
converge en distribución a
una N[0,1]
de donde 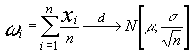 : es decir , que la media aritmética de un
gran número de variables aleatorias independientes e igualmente distribuidas , con la
misma media y varianza ; se distribuirá normalmente con media la media común y ,
desviación típica , la desviación típica común dividida por raíz de n.
: es decir , que la media aritmética de un
gran número de variables aleatorias independientes e igualmente distribuidas , con la
misma media y varianza ; se distribuirá normalmente con media la media común y ,
desviación típica , la desviación típica común dividida por raíz de n.
La gran importancia de esta convergencia y forma del teorema , radica en su aplicabilidad en la relación muestra-población , y así podemos establecer que : "sea cual fuere la distribución de la población, si extraemos una muestra aleatoria de suficiente tamaño, y de forma que las extracciones sean independientes entre sí; la media de esta muestra tiende a una normal, con media la media de la población, y desviación típica, la desviación típica de la población dividida por la raíz del tamaño muestral".