INSESGADEZ
un estimador es insesgado o centrado cuando verifica que
E(
) = 
. (Obsérvese que deberíamos
usar (x)
y no , pues hablamos de estimadores y no de estimaciones pero como no cabe
la confusión ,para simplificar , aquí , y en lo sucesivo usaremos ) . En caso contrario se dice
que el estimador es sesgado . Se llama sesgo a
[se designa con B de BIAS ,sesgo en inglés]
Como ejemplo podemos decir que : la media muestral es un estimador insesgado de la media de la población (y lo es sea cual fuere la distribución de la población) ya que:
si el parámetro a estimar es
y establecemos como estimador de
tendremos que 
luego la
media muestral es un estimador insegado de la media poblacional.
En cambio la varianza muestral es un estimador
sesgado de la varianza de la población , ya que: si utilizamos como estimador de 
la varianza muestral 
es decir : 
tendremos que 
que es el
parámetro a estimar .
existe pues un sesgo que será
Dado que la varianza muestral no es un estimador de la varianza poblacional con propiedades de insesgadez , conviene establecer uno que si las tenga ; este estimador no es otro que la cuasivarianza muestral , de ahí su importancia ;así
la cuasivarianza es en función de la varianza
y tomada como estimador
tendríamos que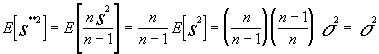 
dado que la esperanza del estimador coincide con el parámetro a estimar podemos decir que la cuasivarianza muestral es un estimador insesgado de la varianza de la población.
No obstante , y dado que ,cuando el tamaño de la muestra tiende a infinito el sesgo tiende a cero, se dice que el estimador es asintóticamente insesgado o asintóticamente centrado: podemos establecer que :
Por tanto la
varianza muestral es un estimador sesgado pero asintóticamente insesgado de la varianza
de la población.