2. PROPIEDADES DE LOS ESTIMADORES

ir a estimación

INSESGADEZ: un estimador es insesgado o centrado cuando verifica que

       E( ) = . (Obsérvese que deberíamos usar (x)    y    no  , pues hablamos de estimadores y no de estimaciones pero como no cabe la confusión ,para simplificar ,  aquí  , y en lo sucesivo usaremos ) . En caso contrario se dice que el estimador es sesgado . Se llama sesgo a  B( ) = - E()  
                                                                                                                [se designa con B de BIAS ,sesgo en inglés]

Como ejemplo podemos decir que : la media muestral es un estimador insesgado de la media de la población (y lo es sea cual fuere la distribución de la población) ya que:

si el parámetro a estimar es

y establecemos como estimador de            

          tendremos que luego la media muestral es un estimador insegado de la media poblacional.

En cambio la varianza muestral es un estimador sesgado de la varianza de la población , ya que: si utilizamos como estimador de la varianza muestral es decir :

                     tendremos que que es el parámetro a estimar .

                                    existe pues un sesgo que será

Dado que la varianza muestral no es un estimador de la varianza poblacional con propiedades de insesgadez , conviene establecer uno que si las tenga ; este estimador no es otro que la cuasivarianza muestral , de ahí su importancia ;así

la cuasivarianza es en función de la varianza               y tomada como estimador

                    tendríamos que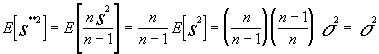

dado que la esperanza del estimador coincide con el parámetro a estimar podemos decir que la cuasivarianza muestral es un estimador insesgado de la varianza de la población.

No obstante , y dado que ,cuando el tamaño de la muestra tiende a infinito el sesgo tiende a cero, se dice que el estimador es asintóticamente insesgado o asintóticamente centrado: podemos establecer que :

                                             Por tanto la varianza muestral es un estimador sesgado pero asintóticamente insesgado de la varianza de la población.

CONSISTENCIA . Un estimador es consistente si converge en probabilidad al parámetro a estimar . Esto es:

                si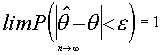              

LINEALIDAD. Un estimador es lineal si se obtiene por combinación lineal de los elementos de la muestra ; así tendríamos  que un estimador lineal sería :

EFICIENCIA. Un estimador es eficiente u óptimo cuando posee varianza mínima o bien en términos relativos cuando presenta menor varianza que otro . Quedando claro que el hecho puede plantearse también en términos más coherentes de Error Cuadrático Medio (ECM). Tendríamos que :

                                  ECM( ) =

   por lo expresado podemos aventurar que un estimador insegado , luego  

es el único capaz de generar eficiencia. (ir a cota de Cramer-Rao)

SUFICIENCIA . Un estimador es suficiente cuando            no depende del parámetro a estimar .
En términos más simples : cuando se aprovecha toda la información muestral.  (ir a teorema de caracterización de Neyman-Fisher)