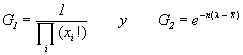Suficiencia.Caracterización de Neyman-Fisher

ir a propiedades de los estimadores

ir a estimación

Para comprobar si un estimador es suficiente respecto de la estimación de un determinado parámetro se puede utilizar el teorema de caracterización de Neyman-Fisher que establece que para que un estimador sea suficiente para q debe cumplirse que:

donde tanto la función G₁, como la G₂, son no negativas y donde G₁ sólo depende de la muestra (no del estimador ni del parámetro) y donde G₂ depende del parámetro a estimar y de su estimador

EJEMPLO:

Comprobar si la media muestral, , de un M.A.S sobre una población de Poisson X® P [ l ] , es un estadístico SUFICIENTE para l .

Según el Teorema de Caracterización de Neyman-Fisher para que un estimador sea suficiente para q debe cumplirse que:

con G₁ y G₂ no negativas , G₁ sólo dependiente de la muestra y G₂ dependiendo del parámetro y del estimador

Veamos que ocurre en nuestro caso:

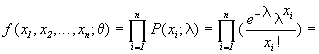
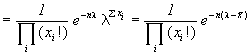
comprobando que la f. de cuantía conjunta de la muestra queda factorizada en dos funciones G₁ y G₂ no negativas y tales que G₁ sólo depende de la muestra y G₂ depende del parámetro y del estimador ; con: