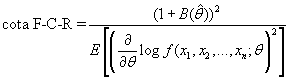
Cota de Cramer-Rao
ir a propiedades de los estimadores
Se puede considerar que un estimador de un parámetro es eficiente en sentido absoluto si tiene menor error cuadrático medio que cualquier otro estimador del parámetro que estamos considerando.
Así pues como el ECM de un estimador es la suma de su varianza y del cuadrado de su sesgo un estimador que :
Sea insesgado
Y que tenga la mínima varianza posible
Será el estimador ÓPTIMO.
Es posible determinar si un estimador tiene mínima varianza ya que la varianza de cualquier estimador siempre es igual o inferior a una cota conocida con el nombre de Cota de Frechét-Cramer-Rao cuya espresión es:
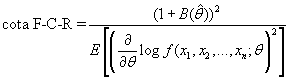
El denominador de esta expresión llamado Información de Fisher de la muestra puede simplificarse en el caso de M.A.S. obedeciendo a la expresión:
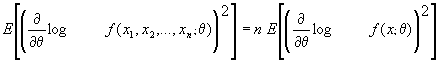
determinar si la media muestral, 
, de un M.A.S. es un estimador óptimo de la media, m , de una
población normal ( X ® N [ m ; s ] )
la media muestral de un M.A.S sobre una población normal se distribuye
® N [ m ; s /Ö n ] ,
por tanto es INSESGADO.
Veamos si su varianza alcanza la cota de Frechét-Cramer-Rao:
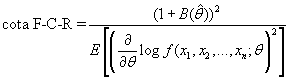
En nuestro caso
= 
=
= 0 y ,por tratarse
de un M.A.S. sobre una población normal, la función de información de Fisher quedará
como:
=
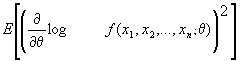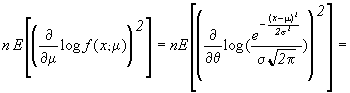
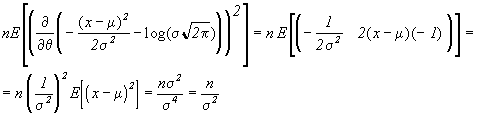
por lo que la cota F-C-R =
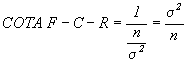
y la varianza del estimador coincide con
ella y , por lo tanto es ÓPTIMO.