MÉTODOS DE ESTIMACIÓN

MÉTODO POR ANALOGÍA. Consiste en aplicar la misma expresión formal del parámetro poblacional a la muestra , generalmente , estos estimadores son de cómoda operatividad , pero en ocasiones presentan sesgos y no resultan eficientes . Son recomendables , para muestras de tamaño grande al cumplir por ello propiedades asintóticas de consistencia.

METODO DE LOS MOMENTOS. Consiste en tomar como estimadores de los momentos de la población a los momentos de la muestra . Podríamos decir que es un caso particular del método de analogía. En términos operativos consiste en resolver el sistema de equivalencias entre unos adecuados momentos empíricos(muestrales) y teóricos(poblacionales).

Ejemplo :

conocemos que la media poblacional de una determinada variable x depende de un parámetro K que es el que realmente queremos conocer (estimar). Así

                               por el método de los momentos tendríamos que

                                   de donde     

ESTIMADORES MAXIMO-VEROSIMILES. La verosimilitud consiste en otorgar a un estimador/estimación una determinada "credibilidad" una mayor apariencia de ser el cierto valor(estimación) o el cierto camino para conseguirlo(estimador).

En términos probabilísticos podríamos hablar de que la verosimilitud es la probabilidad de que ocurra o se dé una determinada muestra si es cierta la estimación que hemos efectuado o el estimador que hemos planteado.

Evidentemente , la máxima verosimilitud , será aquel estimador o estimación que nos arroja mayor credibilidad .En situación formal tendríamos :

Un estimador máximo-verosímil es el que se obtiene maximizando la función de verosimilitud (likelihood) de la muestra

Que es la función de probabilidad (densidad o cuantía) que asigna la probabilidad de que se obtenga una muestra dependiendo del (o de los)parámetro(s) " "    pero considerada como función de .   Si la distribución de la población es tal que su densidad depende de uno o más parámetros   ,   la probabilidad (densidad) de cada realización muestral x_i 
    (con i=1,2,..,n) será:      y, a partir de aquí podremos obtener la función de verosimilitud de la muestra

Si el muestreo es simple:

por ser independientes cada una de las realizaciones muestrales.

El estimador que maximice        

             será el estimador máximo-verosímil (E.M.V.) Y será aquel valor/expresión para el que se verifique la derivada :

             Si lo planteado fuera EMV de varios parámetros      

las expresiones serían. .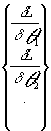

Debido a que la función de verosimilitud es a fin de cuentas una función de probabilidad ,será una función definida no negativa y por lo tanto alcanzará su máximo en los mismos puntos que su logaritmo . Por esta razón suele maximizarse

en lugar de la propia función de verosimilitud . Suele hacerse esto en todos aquellos casos en los que la función de verosimilitud depende de funciones exponenciales.