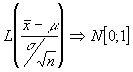
INTERVALO PARA LA MEDIA DE UNA POBLACIÓN NORMAL CON VARIANZA CONOCIDA
ir a
script de realización (con m.a.s)
ir a script de realización ( con irrestricto)
Las circunstancias específicas para la construcción de este intervalo son las siguientes :
Intervalo para m
Conocida s ( o la varianza )
Distribución poblacional normal.
Nivel de confianza dado 1-a
Tamaño muestral desconocido luego nos colocamos en el peor de los casos , es decir pequeño.
Conocemos que la media muestral se distribuye ![]() luego
tipificando
luego
tipificando 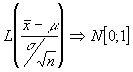
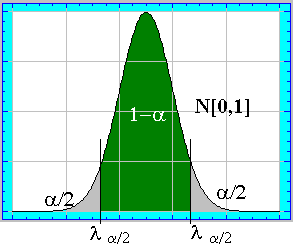 Como se ha comentado ,al ser la normal reducida una distribución simétrica y
unimodal, el intervalo de menor amplitud y de probabilidad
Como se ha comentado ,al ser la normal reducida una distribución simétrica y
unimodal, el intervalo de menor amplitud y de probabilidad
1 - a será el intervalo centrado en la media ,es decir:
el intervalo ![]() . Donde
. Donde ![]() es el valor de la tabla de la N[0 ;1] que haga
que
es el valor de la tabla de la N[0 ;1] que haga
que ![]() Es decir el valor de la normal reducida que deje a su derecha una cola de probabilidad de a /2 Así el valor
Es decir el valor de la normal reducida que deje a su derecha una cola de probabilidad de a /2 Así el valor ![]() será el valor simétrico de
será el valor simétrico de ![]() (con signo negativo) y
dejará a su izquierda una cola de a /2 . De esta forma entre ,
(con signo negativo) y
dejará a su izquierda una cola de a /2 . De esta forma entre ,
![]() y
y ![]() queda
encerrada una probabilidad de 1 - a :
queda
encerrada una probabilidad de 1 - a :
sería así el intervalo de menor amplitud :
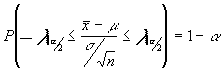 despejando la media poblacional tendríamos :
despejando la media poblacional tendríamos :
![]()
nota : si el muestreo fuera sin reposición , por lo tanto no m.a.s. y si irrestricto ; el intervalo se vería afectado por el factor corrector de poblaciones finitas .Resultando , y sirva este ejemplo para comprobar lo que ocurriría en otros intervalos de otras características, de la siguiente forma : ir a script de realización ( con irrestricto)
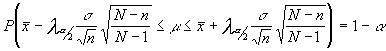 siendo N el tamaño de la población.
siendo N el tamaño de la población.
nota :Aunque no se conozca s (desviación poblacional) si la muestra es bastante grande , n >30 es habitual considerar la desviación típica muestral , S , como si fuera la poblacional y aplicar el intervalo de estimación obtenido arriba.
ejemplo 2
Realizar la estimación de µ del ejemplo 1 considerando ahora que la población es normal
Tendríamos 1-a
=0.95 luego a =0.05 ; S=10=s
(muestra grande n>30); n=2000 ;
![]() ; población normal.
; población normal.
Aplicando el intervalo anterior :
![]()
el resultado sería : µ Î [224'56 , 225'44] con
el 95 % de confianza.