con varianza conocidaCONTRASTAR QUE LA DIFERENCIA DE DOS MEDIAS TOMA UN DETERMINADO VALOR , CON POBLACIONES NORMALES Y VARIANZAS CONOCIDAS O MUESTRAS GRANDES
conocemos que con varianza conocida
conocemos también que 
con varianza conocida
siendo los tamaños muestrales nx y ny se formaliza la hipótesis a contrastar como :
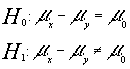
con nivel de significación a
conocemos que la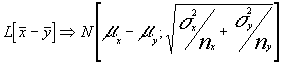 
luego bajo la hipótesis
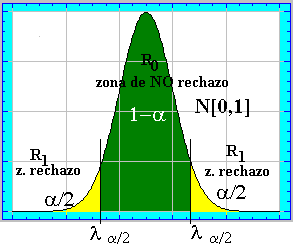
de manera que para un valor concreto del nivel de significación tendremos que las zonas de decisión para el estadístico serán :
T=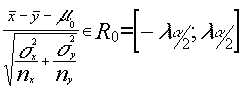
NO rechazamos la hipótesis nula
T=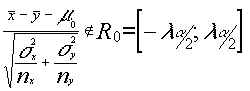
rechazamos hipótesis nula , aceptando H1
Para comprobar si dos máquinas producen tornillos de la misma longitud se recoge una muestra aleatoria de 40 piezas producidas por la máquina A y 50 por la máquina B . Resultando que la media de las 40 piezas de A es de 10 cm. mientras que la de las 50 de B es de 9.5 cm. siendo las desviaciones típicas de las dos muestras 1 y 2 cm . respectivamente. Contrastar con un nivel de significación del 2% la hipótesis de que ambas máquinas fabrican piezas con la misma longitud media.
La hipótesis planteada será :
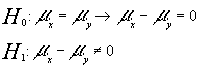Nivel de significación 0.02 por lo
que la zona de no rechazo según tablas de la N[0 ;1]
(ir a tabla de la normal) quedaría R0=[-2.33 ;2.33] siendo el estadístico T
T=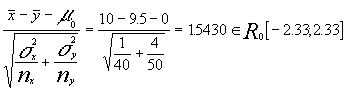
por lo
que No rechazamos la igualdad de medias en la longitud de las piezas producidas por ambas
máquinas
