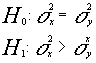para un determinado nivel de significación y con tamaños
muestrales nx para la variable X y ny para la variable Y de manera
que conocemos que :CONTRASTE DE IGUALDAD DE VARIANZA EN POBLACIONES NORMALES
Contrastaremos la hipótesis nula de que las varianzas de dos variables X e Y son iguales frente a la alternativa de que la varianza de X es mayor a la de Y , Tomando como variable X aquella cuya varianza muestral sea mayor.
El contraste quedaría definido :
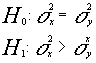para un determinado nivel de significación y con tamaños
muestrales nx para la variable X y ny para la variable Y de manera
que conocemos que :
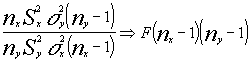bajo la hipótesis
nula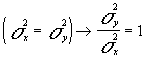 
luego tendríamos que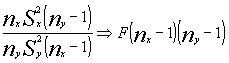 
Para un nivel de significación a tendremos :
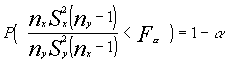
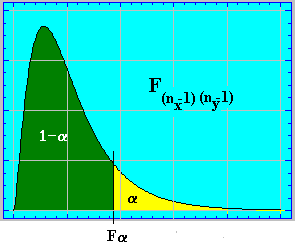
donde Fa es el valor crítico de las tablas para
nx-1 grados de libertad en el numerador y ny-1 grados de libertad en
el denominador y un nivel de significación a
luego , en definitiva el contraste quedaría :
si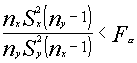 
No rechazamos la hipótesis de igualdad de varianzas
si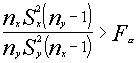 
Rechazaríamos la hipótesis de igualdad de varianzas aceptando la
alternativa , por tanto , varianza de X superior a varianza de Y
Contrastar la hipótesis de que dos poblaciones tienen la misma dispersión con un nivel de significación del 1 % y sabiendo que la desviación típica de una de una muestra realizada sobre la primera población era 12 con un tamaño muestral de 25 y que en una muestra sobre la segunda de tamaño 30 la desviación típica resultó ser 7 .
Considérese que ambas poblaciones son normales.
El contraste sería : 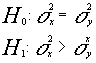conocemos que el nivel de significación es 0.01
y : 
tomando cómo X la de mayor varianza muestral el estadístico T será :
T=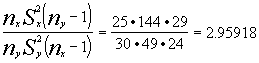
el valor de 
(ir a tabla de la F de Snedecor)
dado que T > Fa 2.95918>2.49 rechazamos igualdad de varianzas aceptando que la primera tiene una varianza mayor .