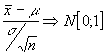
CONTRASTAR QUE LA MEDIA DE UNA POBLACIÓN NORMAL TOMA UN DETERMINADO VALOR
ir a contrastes
ir a script de realización
Deseamos contrastar la hipótesis de que el parámetro poblacional q = m toma un
determinado valor m 0 . Conocemos que la población
se distribuye normalmente y conocemos también su varianza , o bien si nos es desconocida
,el tamaño muestral es lo suficientemente grande
cómo para poder utilizar la muestral cómo poblacional.
Hemos determinado un nivel de significación para la realización del contraste y vamos a
plantearlo en el supuesto de realizar una muestra aleatoria de tamaño n.
así : conocemos que ![]() de lo que deducimos
que
de lo que deducimos
que 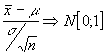
de forma que bajo la hipótesis nula : ![]() tendremos
el intervalo.
tendremos
el intervalo.
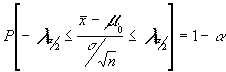 realizada la muestra y conocidas n y
realizada la muestra y conocidas n y ![]()
conoceremos el valor T del estadístico T=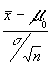 de manera que establecemos
de manera que establecemos
si T =
No rechazamos
si T =
rechazamos
donde como ya es conocido![]() es el valor de la N[0 ;1] para el que se verifica que
es el valor de la N[0 ;1] para el que se verifica que
![]()
![]()
en caso de ser el muestreo irrestricto sería
de aplicación el f.c.p.f : ir
a script de realización
De 100 observaciones de una población normal se obtiene que ![]() = 5 y que S
=2.Contrastar con un nivel de significación del 5% la hipótesis de que la media de la
población sea 7.
= 5 y que S
=2.Contrastar con un nivel de significación del 5% la hipótesis de que la media de la
población sea 7.
( ir a script de realización)
Tendremos que : H0 : m =7
H1 : m ¹ 7
conocemos que a =0.05
![]() S= 2 n=100 (mayor que 30) luego podemos
tomar s = S= 2 el estadístico T
S= 2 n=100 (mayor que 30) luego podemos
tomar s = S= 2 el estadístico T
será T= 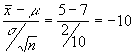
la
región o zona de no rechazo para a =0.05 será ![]() =[-1’96 ;1’96]
(ir a tabla de la Normal)
=[-1’96 ;1’96]
(ir a tabla de la Normal)
dado que T=-10 no pertenece a la región de aceptación estamos en condiciones de rechazar la hipótesis nula luego aceptar la alternativa : m ¹ 7