bajo la hipótesis planteada 
tendremos
que 
CONTRASTAR QUE LA MEDIA DE UNA POBLACIÓN TOMA UN DETERMINADO VALOR CON POBLACIÓN NORMAL , MUESTRA PEQUEÑA , Y VARIANZA DESCONOCIDA
ir a contrastes
ir a script de
realización
Deseamos contrastar la hipótesis de que el parámetro poblacional q = m toma un determinado valor m 0 .Desconocemos la varianza de la población y, dado que el tamaño muestral es pequeño , no podemos utilizar la muestral en su lugar.
Hemos determinado un nivel de significación para la realización del contraste y vamos a plantearlo en el supuesto de realizar una muestra aleatoria de tamaño n.
Conocemos que
bajo la hipótesis planteada tendremos
que
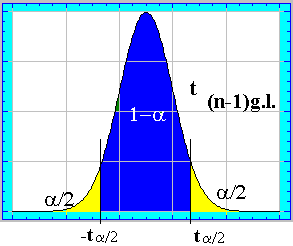
Donde 
es el valor de
la tabla de la t de Student de (n-1) grados
de libertad tal que cumple lo que se explicita en la imagen contigua.
Partiendo del intervalo expuesto y concretada la muestra obtendremos el estadístico T
tal que T=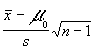
de manera
que si el estadístico T ::
Si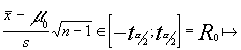 
No rechazamos la hipótesis
Si T=
Rechazamos la hipótesis
en caso de ser el muestreo irrestricto sería de aplicación el f.c.p.f : ir a script de realización
ejemplo 2.
Se escoge a 17 individuos al azar y se les mide resultando que su estatura media es de 1,71 metros con desviación típica de 0,02 .Contrastar la hipótesis de que la estatura media nacional sea de 1.75 metros si utilizamos un nivel del significación del 5%. Se supone normalidad (ir a script de realización)
Conocemos que n=17 a =0,05 
S=0,02
deseamos contratar H0: m =1,75
H1: m ¹ 1,75
para una t de Student de n-1=16 g.l tendremos que 
(ir a tabla de t
de student)
por lo que el estadístico será
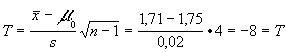
dado que -8=TÏ [-2,12;2,12] luego rechazamos la hipótesis nula m =1,75