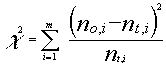
CONTRASTES DE LA BONDAD DEL AJUSTE
ir a contrastes no
paramétricos
ir a script de realización
También se le conoce como contraste de adherencia a un ajuste, o como contraste de la c 2.
La hipótesis a contrastar es el hecho (nótese que no hay valor de un
parámetro) de que la muestra proviene de una distribución determinada y planteada de
probabilidad , frente a la alternativa de que esto no es así .
Se parte de una sola muestra (lógico) normalmente en datos en forma de escala nominal ,
de ahí que este test se encuentre ubicado donde los está en la tabla resumen que antes
presentamos
A través de este contraste, y partiendo de los datos muestrales , se obtiene un criterio
de decisión sobre la hipótesis de que la población de la que se ha extraído la muestra
se distribuya ( se ajuste bien , se adhiera ), o no , según algún modelo teórico
determinado y planteado a priori. Así :
H0 : la muestra proviene(ajusta ,adhiere) a una
población cuya función es (F(x))
H1 : la muestra NO proviene(ajusta ,adhiere) a una población cuya
función es (F(x))
y trabajando con un determinado nivel de significación plantearíamos
que si:
Las observaciones muestrales podremos considerarlas y disponerlas como una distribución de frecuencias ;frecuencias
, claro está ,observadas.
xi |
nobservadas,i |
x1 |
no,1 |
x2 |
no,2 |
· |
· |
xm |
no,m |
Si la población sigue un determinado modelo teórico de distribución de probabilidad cada posible valor de la variable xi tendrá asociada una determinada probabilidad , según ese modelo teórico.
Para cada uno de los valores muestrales podremos construir su distribución de probabilidad:
xi |
P(xi) |
x1 |
P1 |
x2 |
P2 |
· |
· |
xm |
Pm |
Si multiplicamos, para cada xi , su probabilidad , Pi , por el número total de observaciones, n , obtendremos las frecuencias que teóricamente debían corresponder a cada valor de la variable, según el modelo, (Pi·n = n teórica,i ).
Y, así , podremos construir una distribución de frecuencias teóricas:
xi |
nteóricas,i |
x1 |
nt,1 |
x2 |
nt,2 |
· |
· |
xm |
nt,m |
A partir de la distribución de frecuencias observadas y de la de frecuencias teóricas puede construirse el siguiente estadístico:
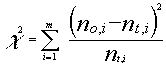
![]() donde m es el número de
valores de la variable que se han muestreado (valores distintos)
donde m es el número de
valores de la variable que se han muestreado (valores distintos)
Puede demostrarse que si la distribución de la población es
efectivamente la utilizada para construir las frecuencias teóricas, el estadístico
anterior se distribuye como una![]() es decir una chi-dos con m-k-1 grados de libertad, donde k es el número de
paramétros estimados a partir de los datos muestrales y necesarios para la construcción
de la tabla de frecuencias de la distribución teórica.
es decir una chi-dos con m-k-1 grados de libertad, donde k es el número de
paramétros estimados a partir de los datos muestrales y necesarios para la construcción
de la tabla de frecuencias de la distribución teórica.
La pérdida de k+1 grados de libertad se debe precisamente a que con los m datos se
calculan k parámetros (habrá ,por tanto, k ecuaciones que liguen los m datos) y ,
además, la suma de los m datos debe dar el número total de observaciones n (lo que
supone una nueva ligadura):
m grados de libertad iniciales - (k + 1) ligaduras = m-k-1 grados de libertad finales
Debe observarse que este estadístico se distribuye siempre como una c 2m-k-1 sea cual fuere el modelo teórico ( binomial, Poisson ,normal ,exponencial ,cualquiera de los estudiados, u otro diseñado "ad hoc"), siempre y cuando la población se distribuya, efectivamente, según ese modelo.
Teniendo en cuenta esto ,si queremos contrastar la hipótesis de que una cierta población sigue un modelo determinado, con un nivel de significación a , habrá que diseñar una región crítica según la cual si los datos muestrales nos conducen (bajo el supuesto de la hipótesis) a un estadístico c 2 que pertenezca a ella rechazaremos la hipótesis.
Según la definición de nivel de significación a se habrá de cumplir que:
![]()
donde ![]()
 Como siempre, de todas las posibles regiones que cumplen esa condición, escogeremos
aquella que tenga mayor amplitud (lo que supone mayor amplitud de la zona de rechazo y, en
consecuencia menor amplitud de la zona de aceptación) para poder realizar un contraste
severo.
Como siempre, de todas las posibles regiones que cumplen esa condición, escogeremos
aquella que tenga mayor amplitud (lo que supone mayor amplitud de la zona de rechazo y, en
consecuencia menor amplitud de la zona de aceptación) para poder realizar un contraste
severo.
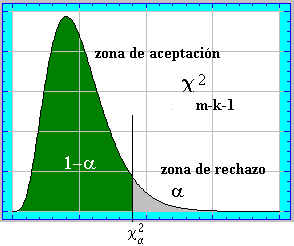
Teniendo en cuenta que el estadístico sigue una distribución c 2 , la región crítica de mayor amplitud será la cola de la derecha.
Así pues, una vez calculado el estadístico c 2 si:
![]() no rechazaremos la
hipótesis de que la población sigue el modelo de probabilidad planteado . ;
mientras que si :
no rechazaremos la
hipótesis de que la población sigue el modelo de probabilidad planteado . ;
mientras que si :
![]() rechazaremos la
hipótesis
rechazaremos la
hipótesis
Por último quedan hacer dos observaciones finales sobre este contraste:
El estadístico c 2 se calcula a partir de conteos discretos de las frecuencias para cada posible valor de la variable y ,como es bien sabido, la distribución c 2 es una distribución de variable continua. Si las frecuencias esperadas para todos los valores de la variable nteóricas,i " i son grandes , este hecho no plantea problemas.
Pero si alguna de las frecuencias teóricas es inferior a 5 será necesario subsanar este inconveniente agrupando las observaciones adyacentes. A modo de ejemplo :
en esta tabla existen frecuencias inferiores a 5
x |
nobservadas,i |
nteóricas,i |
·· |
·· |
·· |
xi |
6 |
4 |
xi+1 |
1 |
2 |
·· |
lo que resolveríamos de la siguiente forma
x |
nobservadas,i |
nteóricas,i |
·· |
·· |
·· |
xi+xi+1 |
6+1=7 |
4+2=6 |
·· |
 Por otro lado, cuando resulta que los grados de libertad
implicados son sólo 1 (es decir, m-k-1 = 1) el estadístico c 2
toma un sobrevalor que "infla" la rechazabilidad de la hipótesis , dado que la
distribución chi-dos con un solo grado de libertad se eleva de forma evidente en la parte
próxima a cero haciendo que el valor crítico, que divide las zonas , sea muy próximo a
éste , primando, por ello, la rechazabilidad de la hipótesis . Para paliar esto, el
americano Yates probó que es
conveniente cuando m-k-1 = 1 utilizar como estadístico el siguiente :
Por otro lado, cuando resulta que los grados de libertad
implicados son sólo 1 (es decir, m-k-1 = 1) el estadístico c 2
toma un sobrevalor que "infla" la rechazabilidad de la hipótesis , dado que la
distribución chi-dos con un solo grado de libertad se eleva de forma evidente en la parte
próxima a cero haciendo que el valor crítico, que divide las zonas , sea muy próximo a
éste , primando, por ello, la rechazabilidad de la hipótesis . Para paliar esto, el
americano Yates probó que es
conveniente cuando m-k-1 = 1 utilizar como estadístico el siguiente :
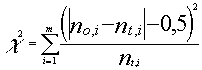
Estas dos puntualizaciones deberán tenerse presentes a la hora de realizar los contrastes de adherencia a un ajuste (hipótesis: Población sigue cierto modelo), así como al realizar los contrastes de independencia (tablas de contingencia que estudiaremos después, cuando sean oportunas - son lo que se conoce como correcciones de continuidad de la prueba o test de la c 2.