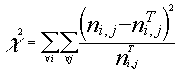
CONTRASTE DE INDEPENDENCIA

ir a contrastes no paramétricos

ir a script de realización

A través de este contraste pretendemos probar si existe independencia entre dos variables o atributos (en el conjunto de la población) a partir de las observaciones de las dos característica (en una muestra).Se trata, en realidad, de un caso particular del contraste de adherencia a un ajuste, en el que el modelo teórico sujeto a contraste es el de una distribución bidimensional con variables independientes.

Las frecuencias observadas las podemos disponer en una tabla de contingencia:

Donde : n_i,j es la frecuencia conjunta

n_i,* es la frecuencia marginal de x

n_*,j es la frecuencia marginal de y

Si la hipótesis de independencia se cumple, y por el teorema de caracterización , se deberá cumplir que todas las frecuencias relativas conjuntas sean iguales al producto de las respectivas frecuencias relativas marginales:

luego en el caso de independencia cada una de las ij frecuencias conjuntas teóricas serán : si establecemos el mismo método del test de la chi-2 crearemos el estadístico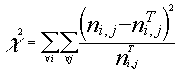

hay que puntualizar que el citado estadístico se distribuirá con una distribución   c ² con (m-1)(n-1) grados de libertad.

Las frecuencias conjuntas debe verificar siempre :

para cada fila

para cada columna

pero además :

una de las m + n ecuaciones anteriores será combinación lineal de las otras m+n-1.

De manera que de los m.n sumandos que constituyen el estadístico
(m.n celdas de la tabla) ,m+n-1 están determinados por los demás y quedan por lo tanto:

m·n -(m+n-1) libres = m·n - m - n + 1 = (m-1).(n-1).

Como no estima ningún parámetro el número de grados de libertad será el número de sumandos (variables) libres (independientes): por tanto el estadístico seguirá     ir a ejemplo