4. Desamos conocer si existe relación entre la edad de nuestros empleados y su rendimiento profesional ; para ello hemos realizado pruebas a 100 de ellos con los resultados siguientes :

rendimiento\ edad menores de 45 mayores de 45
óptimo 12 30
medio 18 40

contrastar dicha hipótesis con nivel de confianza del 94%  
(ir a script de contraste independencia)

El problema radica en realizar un contraste de independencia entre la edad y el rendimiento , si esto es así (independencia) no existirá relación entre ambas , luego :

H0 :existe independencia entre edad y rendimiento
para realizarlo construimos la tabla de contingencia que incluya frecuencias observadas y teóricas :

rendimiento\edad menores 45 mayores 45  
  obs teo obs teo  
óptimo 12 12,6 30 29,4 42
    0,0008   0,0003  
medio 18 17,4 40 40,6 58
    0,0006   0,0002  
  30   70   100

dado que la distribución del estadístico será   ( Ir a  otro script de solución)

c 2 con (m-1)·(n-1) gl. es decir con (2-1)(2-1)=1gl es de aplicación la correción de yates :

calculemos primero las frecuencias conjuntas teóricas.

     y de la misma manera para todas las frecuencias conjuntas teóricas

dado que es de aplicación la corrección de Yates tendremos que cada celda será :

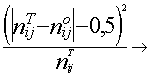     en ese caso    
y así para cada par de frecuencias ; teórica y obsevada siendo el estadístico :

el estadistíco se distribuye como dijimos según una c 2 con 1gl que para a =0,06 toma el valor según tabla (ir a tabla de lac 2)de 3,537. Dado que este valor es mayor que 0,0019     .No podemos rechazar la hipótesis de independencia luego la edad no influye en el rendimiento laboral.