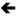Open Office. Calc. Medidas de Tendencia central
Jaione Cubero Ibáñez; Victoria Quesada Serra, Beatriz Gallego Noche; Miguel Ángel Gómez Ruíz; María Soledad Ibarra Sáiz y Gregorio Rodríguez Gómez
Departamento de Didáctica. Área Métodos de Investigación y Diagnóstico en Educación.
Universidad de Cádiz
OpenOffice Calc. Medidas de Tendencia central
Las medidas de tendencia central sirven como puntos de referencia para interpretar las calificaciones que se obtienen en una prueba. Al describir grupos de observaciones, con frecuencia es conveniente resumir la información con un solo número. Este número que, para tal fin, suele situarse hacia el centro de la distribución de datos se denomina medida o parámetro de tendencia central o de centralización.
En ellas encontramos:
* La media o promedio: La media aritmética es el valor obtenido por la suma de todos sus valores dividida entre el número de sumandos. Es, probablemente, uno de los parámetros estadísticos más extendidos. Se le llama también promedio o, simplemente, media.
* La mediana: Es el valor que se ubica en el centro de una distribución. El valor central de un conjunto de valores ordenados en forma creciente o decreciente.
* La moda: Es el valor que se presenta con mayor frecuencia en una distribución, es decir, el valor que más se repite.
* La suma: Suma de todos los valores
Cuando analizamos los datos de una matriz, los primeros análisis a realizar son las medidas de tendencia central y dispersión que nos ayudan a conocer los datos con los que estamos trabajando.
Para calcular la media:
Menú: Insertar
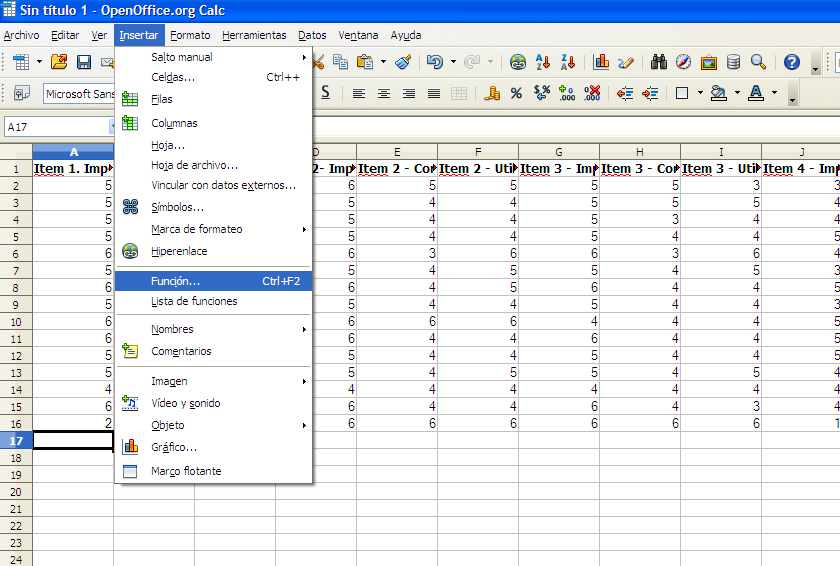
Figura 1. Insertar función
Alternativamente podemos accediendo al asistente de funciones (fx) seleccionando el símbolo que aparece señalado en rojo en la figura 2.
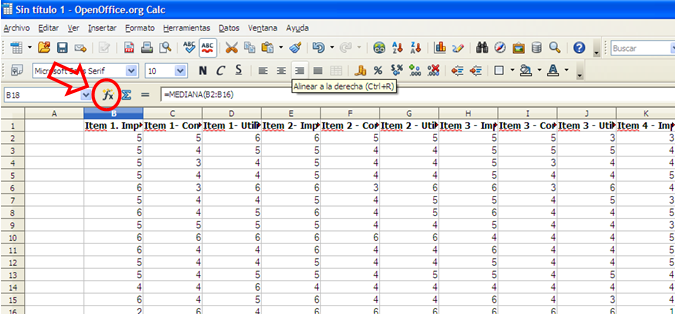
Figura 2. Insertar función
Para calcular la media:
En el asistente de función seleccionamos la función que nos interesa, en este caso PROMEDIO (Ver figura 3)
Figura 3. Insertar función promedio
Una vez localizado es imprescindible hacer doble clic sobre la opción deseada para que el programa lo reconozca.
Posteriormente hay que seleccionar el rango de datos de los que queremos obtener el promedio, para ello, como se puede observar en la figura 4, habrá que seleccionar el siguiente botón: 
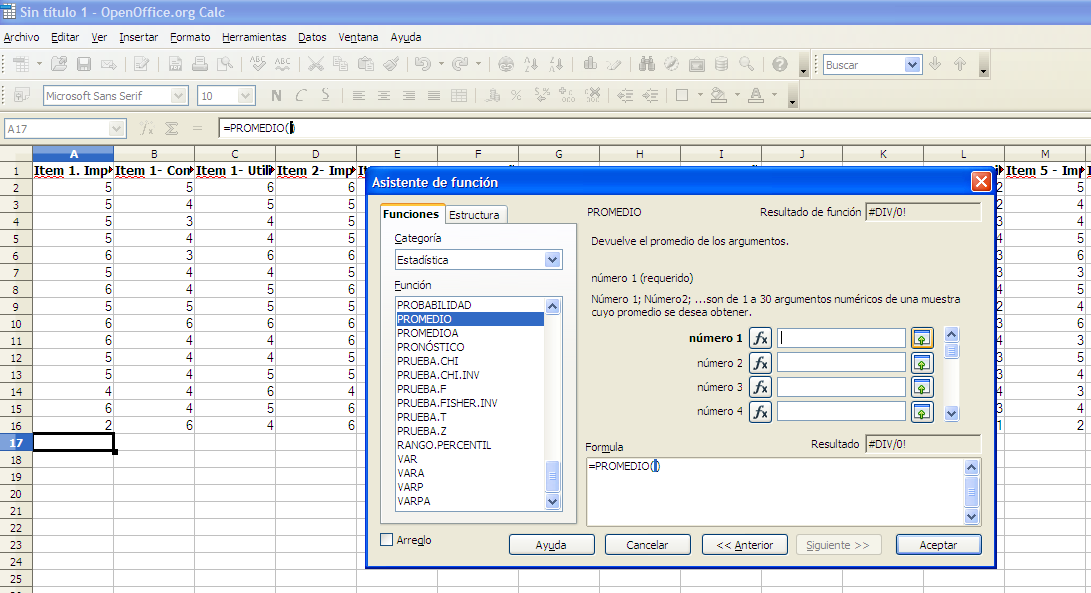
Figura 4. Selección del rango de datos
Entonces, aparecerá el siguiente cuadro, se selecciona el rango de datos con los que queremos trabajar y se vuelve a seleccionar el botón  (Ver figura 5).
(Ver figura 5).
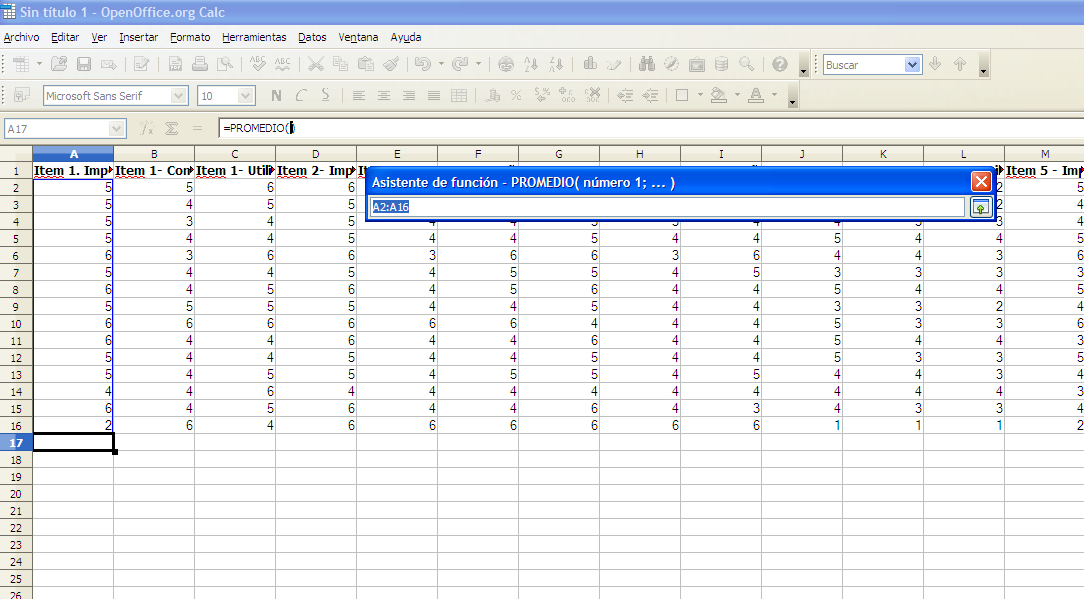
Figura 5. Selección del rango de datos
Aparece a continuación el promedio de los datos, en este caso es de 5.07, como se puede apreciar en la figura 6.
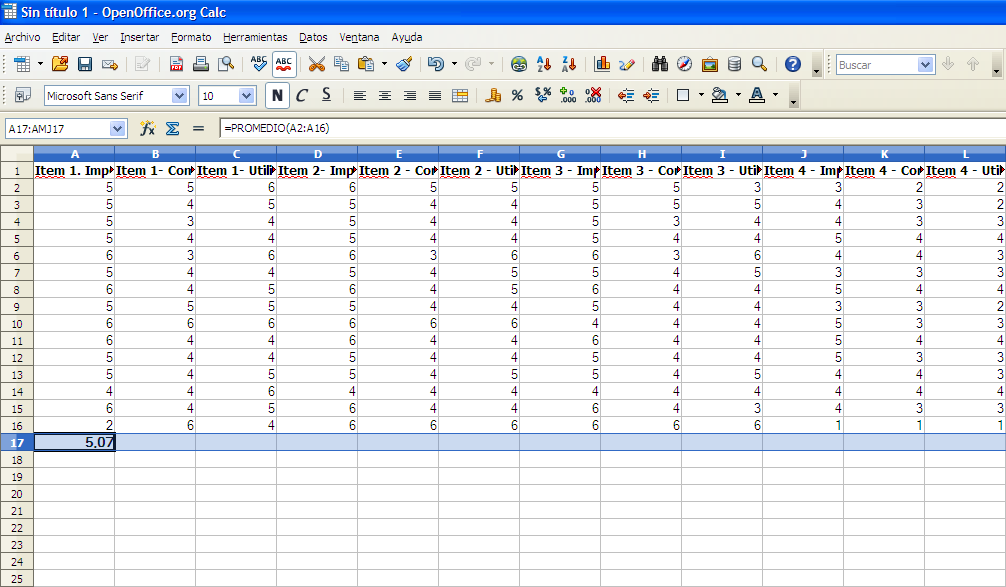
Figura 6. Resultado de la función Promedio
Para calcular la mediana:
Siguiendo el procedimiento anterior
Figura 7. Insertar función
Seleccionamos la función MEDIANA, y el rango de datos con el que queremos trabajar (Ver figura 8).
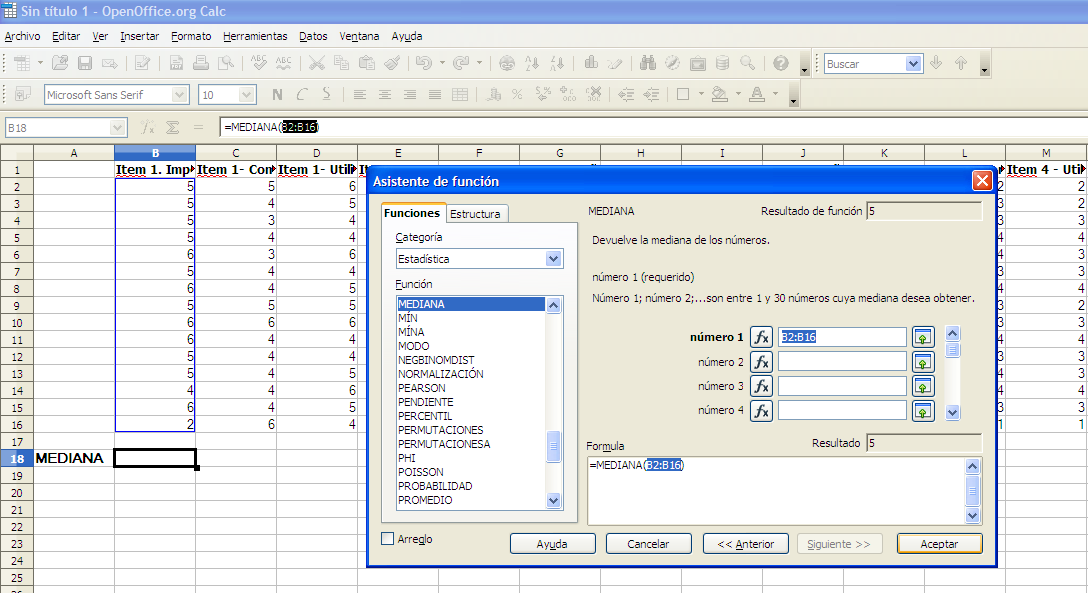
Figura 8. Selección del rango de datos
Como se puede apreciar en la figura 9, la mediana obtiene una puntuación de 5.
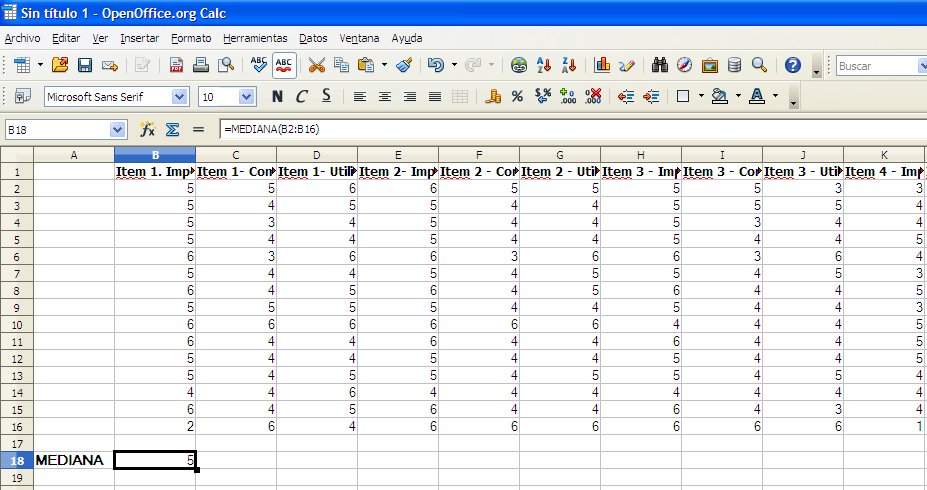
Figura 9. Resultado de la mediana
Para calcular la moda:
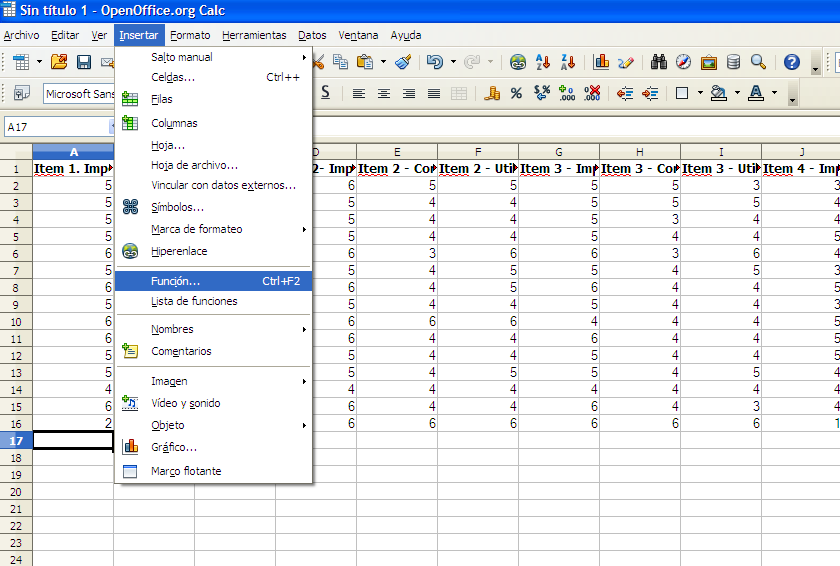
Figura 10. Insertar función
Buscar MODO. Seleccionamos con doble clic y delimitamos el rango de datos con los que queremos trabajar como hemos hecho anteriormente (Ver figura 11).
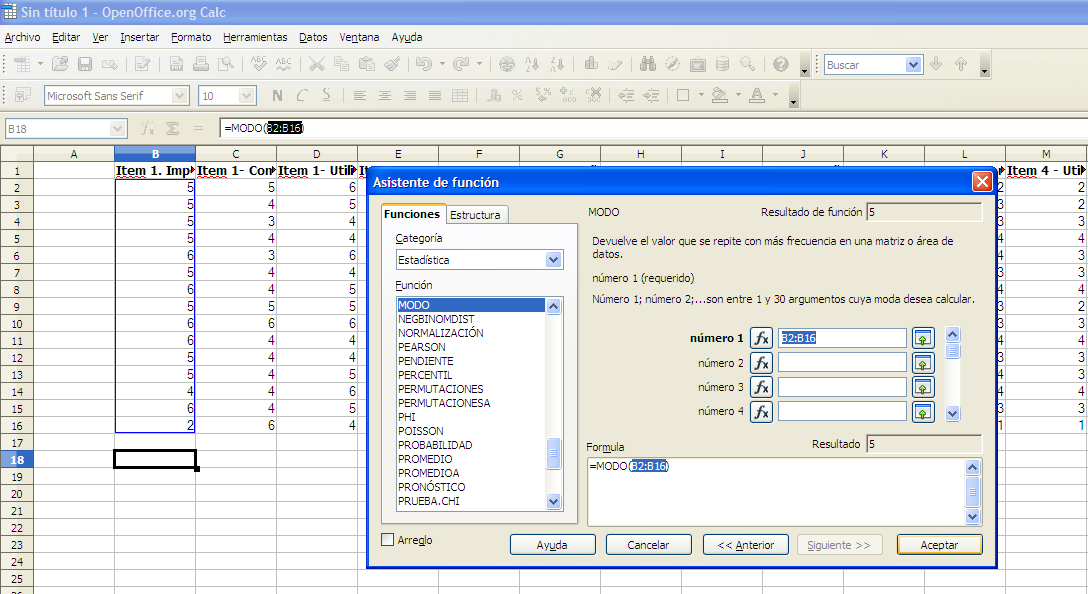
Figura 11. Selección del rango de datos
En este caso podemos comprobar, que el número que mayor veces aparece es el 5 (Ver figura 12).
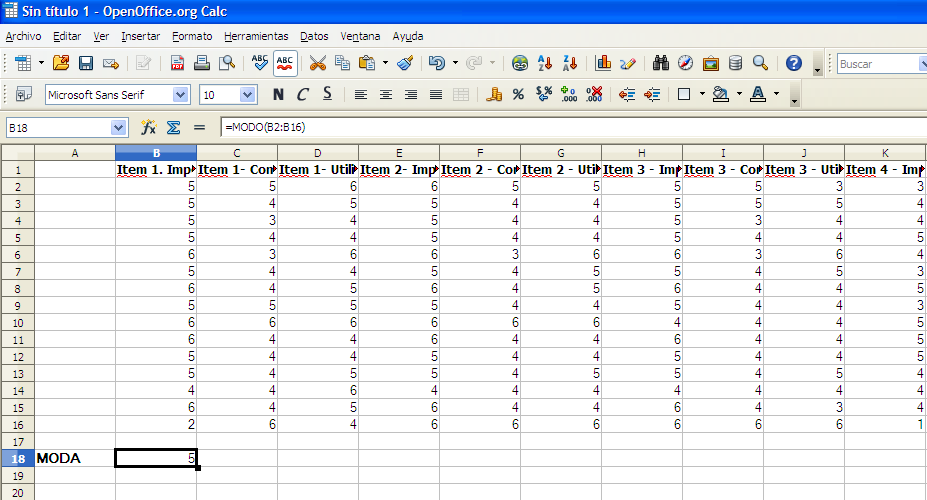
Figura 12. Resultado de la MODA
Para calcular la suma:
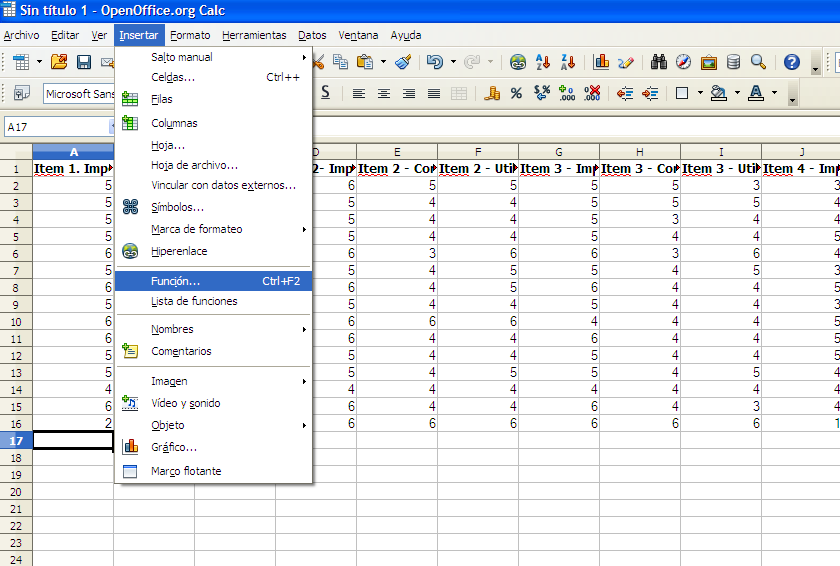
Figura 13. Insertar función
Buscar SUMA. Seleccionamos con doble click y delimitamos el rango de datos que queremos sumar (Ver figura 14).
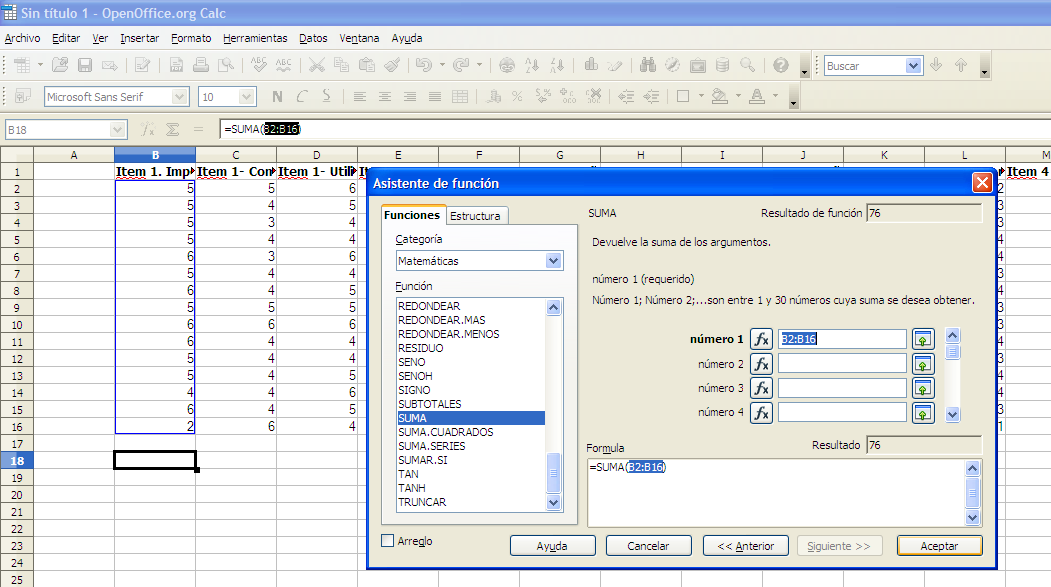
Figura 14. Selección del rango de datos
Para poder aplicar la misma función en todos los ítems o columnas podemos pinchar en el lateral inferior derecho del resultado de la función anterior y arrastrar hacia los diferentes ítems. (Ver figura 15).
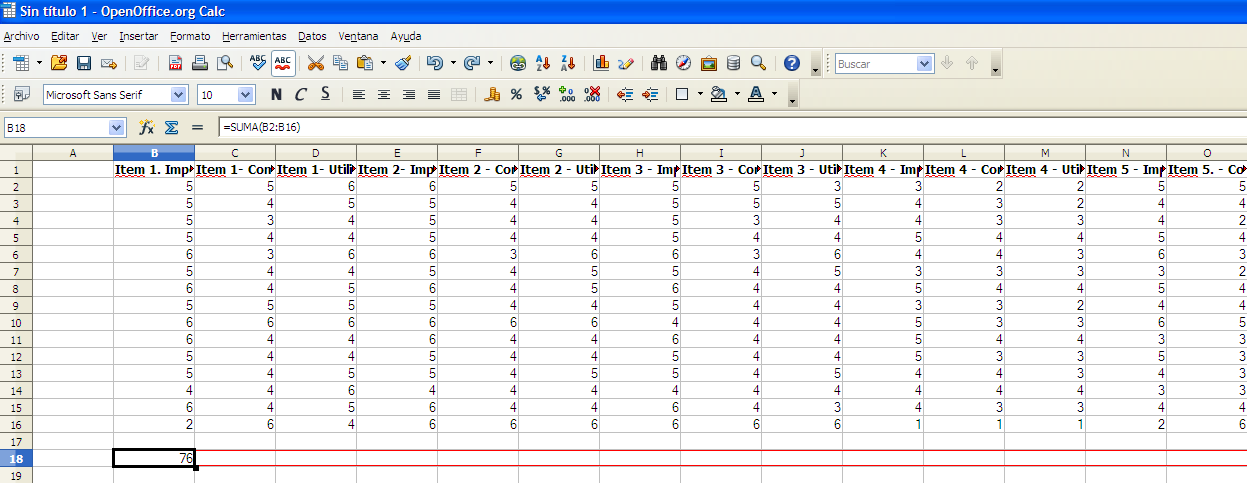
Figura 15. Aplicar la misma función en todas las columnas o ítems
Como se puede apreciar en la figura 16 (destacado en azul), se ha calculado automáticamente la misma función a cada columna o ítem.
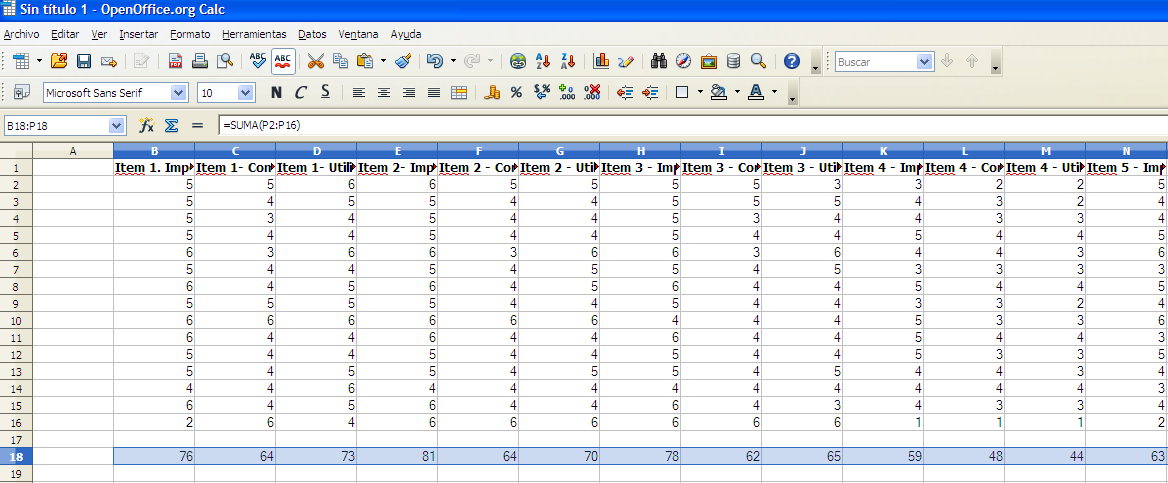
Figura 16. Resultado de la aplicación de la misma función a los diferentes ítems o columnas
Recursos
Ejercicio
 Vídeo
Vídeo
 pdf
pdf



Material elaborado en el marco de la convocatoria de Innovación Educativa y Calidad Docente del Vicerectorat de Cultura, Igualtat I Planificació de la Unviversitat de València de 23 de marzo de 2012