Indice
> Desarrollo de la
práctica> Medida
del aumento visual y del campo visual
Medida por el método indirecto
En este método es necesario el uso de un
“ojo artificial” que reciba la imagen proporcionada por la lupa.
Dicho “ojo” está compuesto por una lente convergente de
focal f '=50
mm que sustituye al acoplamiento córnea-cristalino, y una pantalla
milimetrada que hace las veces de retina.
El tamaño de la imagen “retiniana” es proporcional al tamaño
angular del objeto, por lo que ahora podemos medir el aumento visual simplemente
comparando los tamaños de las imágenes “retinianas”
obtenidas en visión directa y a través de la lupa.
Para comenzar se prepara el dispositivo experimental de la figura siguiente,
situando el objeto en el plano
zo = 0.
La distancia que separa la lupa del “ojo artificial” puede ser
seleccionada arbitrariamente. Sin embargo, con el fin de trabajar en buenas
condiciones de campo visual se propone que sea igual
a 125 mm.
 |
|
|
Al realizar el experimento se observa la imagen que se muestra en la figura siguiente. Para el cálculo del aumento visual es conveniente seleccionar una parte de la escala objeto, por ejemplo una fracción de tamaño y = 20 mm. Seguidamente, se mide, con la escala de la pantalla, el tamaño “retiniano”, y'r, de la imagen del objeto seleccionado. El tamaño angular de la imagen, w', se obtiene aplicando la relación tan w' = y'r /a'r
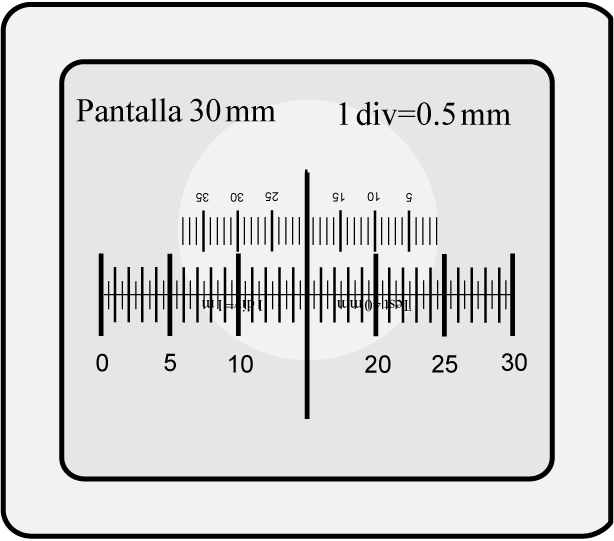
|
A continuación se debe medir el tamaño y'A de la imagen “retiniana” obtenida en visión directa, correspondiente a la misma fracción de objeto seleccionada anteriormente. Para ello se sitúa el objeto a 250 mm de la lente-ojo.
 |
|
|
Al realizar el experimento se observará una imagen similar a la que se muestra en la figura siguiente. A partir de ella puedes medir y'A y evaluar tan wA = y'A / a'A
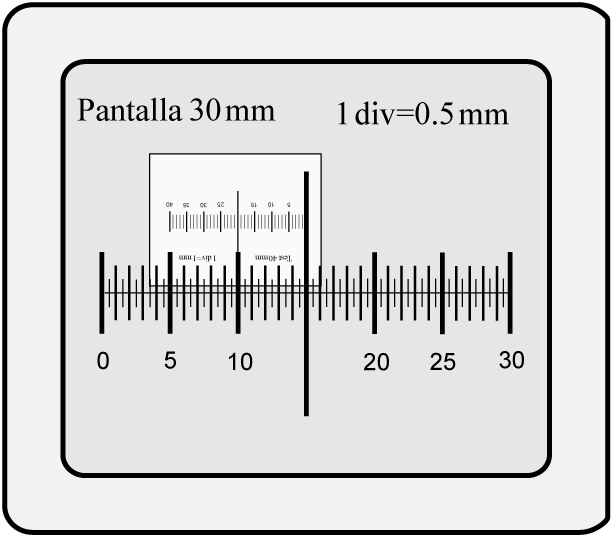
Finalmente el aumento visual se obtiene calculando el cociente tan w' / tan wA
|
Para estudiar la dependencia del aumento y del campo con la posición del objeto repetimos las experiencias anteriores, pero situando el objeto en el plano zo = 25 mm. Ahora para obtener una imagen enfocada del objeto hay que situar la pantalla a la distancia a'r=56.7 mm y la imagen observada será similar a la de la figura siguiente. A partir de ella puedes medir y'r y calcular tan w' = y'r /a'r.
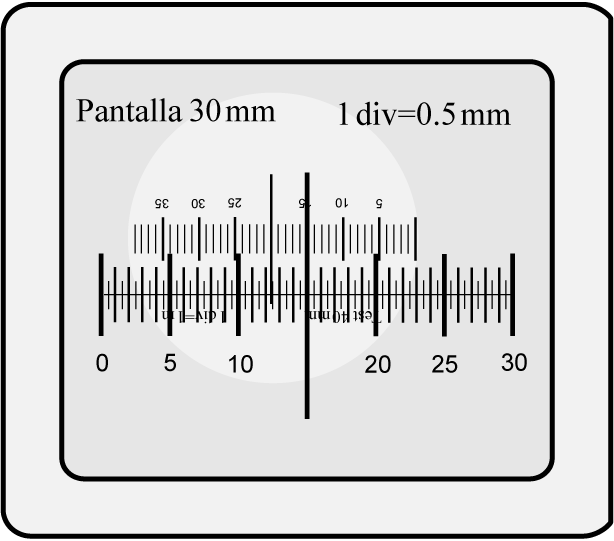
|
![]()