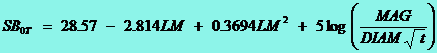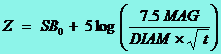![]() On the Prediction of Visibility
for Deep Sky Objects
On the Prediction of Visibility
for Deep Sky Objects
Systems to anticipate
whether a stellar or non‑stellar object will be visible
Knowing in advance the visibility of a given object is
important when planning an observation. New amateurs usually search only bright
objects since they present smaller difficulties for finding and observing them,
except perhaps under severe conditions (e.g., city, full moon). Nevertheless,
amateurs gradually extend their observations to more challenging targets,
fainter and more elusive. These objects, being more difficult, can offer
dramatically different images depending on the telescope aperture and sky
quality. Therefore, to predict with certain accuracy the difficulty that an
observation will involve may become a puzzling task. Most observers estimates
the possibilities of observing a celestial object in a subjective way,
depending on experience in handling their telescopes and knowledge on deep‑sky
objects. It would be however convenient to have a more objective tool to decide
whether a given object will be visible or not.
Plots for
prediction of visibility
Software for the
prediction of visibility
Introduction
For a
long time, the prediction of visibility for deep‑sky objects has been one
of my favorite astronomical topics. The same way as many amateurs, I knew that
many widely extended ideas in this field, stated as true, were indeed quite
unreliable. Points as the convenience of using telescopes with short focal
ratios and very low magnifications, able to concentrate light of diffuse
objects, and questions as the binocular giving the best performance, or the
faintest star visible at a given telescope. Some few works appeared where shyly
the dominant trends imposed by astronomers of unquestionable authority, as
Sidgwick for instance were contradicted. However, nobody dare to disagree.
When Roger Clark's Visual Astronomy of the Deep Sky
(VASDS) was published, many of the thoughts mentioned above became tangible.
VADS represented almost a revolution, a breaking point in visual observational
techniques. In this excellent book, Roger Clark smartly explains all those
ideas that deep‑sky amateurs have in mind, by mere intuition, as we know
better our telescope and we learn to observe. If any of you haven't yet read
VADS, I strongly recommend to do it.
Almost all the published methods to calculate the
visibility of deep‑sky objects are based on the concept of surface
brightness. The surface brightness (SB) is defined as the
brightness, measured in magnitudes, that a given angular surface pertaining to
the studied object presents, supposed uniform, and is given by the following
expression:
|
|
(1) |
where, m represents the object's visual
magnitude, and a, b are the major and minor axes, measured in
convenient angular units. For example, the Crab Nebula, which is 6' ΄ 4' sized and shines with the 8.4 visual
magnitude, would have a surface brightness of 11.6 mag΄arcmin2 (or 20.5 mag΄arcsec2, depending on the
units used for expressing the axis size). One can use arcminutes for a
and b, and however obtain SB in mag΄arcsec2, just adding 8.89 to
the result expressed in mag΄arcmin2. In the present work we'll use mag΄arcsec2 for two reasons. One
is that these units are more convenient taking into account the ordinary
diameters of deep‑sky objects, avoiding thus negative numbers resulting
from the logarithm in Equation 1, which is translated into a SB greater
than the object's magnitude. The second reason is related to the Airy's disk
given by a telescope, whose diameter is quite smaller than one arcmin2,
but closer in magnitude order to one arcsec2, which is useful to
compare with stellar thresholds.
To take into account the object's brightness and size
is a good starting point, but it is not enough. It is also necessary to
consider the brightness of the sky background where the object is projected on.
Sky background severely disturbs our capability to distinguish subtle details.
In the following discussion, we will not consider irregular factors as Milky
Way glow, or zodiacal light. The residual glow of the sky dome, namely the background
surface brightness (SB0), can be evaluated from
calibrates. These calibrates are prepared measuring the fading apparent
diameter of a set of defocused stars with known magnitudes. The visual angle at
which stars are confounded with the sky background is usually taken between 6
and 10 arcminutes for weak images (see Figure 1). Despite that, precise enough
values can be obtained based on the faintest star visible at the naked eye,
through the following polynomial approach:
|
|
(2) |
This
expression is valid for limiting magnitudes at the naked eye (LM)
greater than 5.0. If LM is smaller than 5.0 there is no rodopsine (or visual
purple: the pigment responsible of the greater eye sensitivity during
the night) activation, and our eyes will work as under daylight conditions, but
with a more dilated pupil. The upper limit (8.5 LM) corresponds to a 27
mag΄arcsec2 background
surface brightness: the eye detection threshold. Two drawbacks, however,
prevent us to reach such a faint surface brightness at the naked eye. One is
that the sky is never dark enough; the other is that faint stars are never
really isolated: we are dazzled by their neighboring stars. From best rural
sites we can see up to 7.8 magnitude stars at the naked eye. Under these
conditions, the celestial dome presents a residual brightness of about 24.3 mag΄arcsec2, with small
emission lines at the visible window due to ionized atmospheric gases under
very low pressures (sodium, hidroxile, oxigene, etc.). The maximum background
darkness in the visible light domain is located at 410 nm.
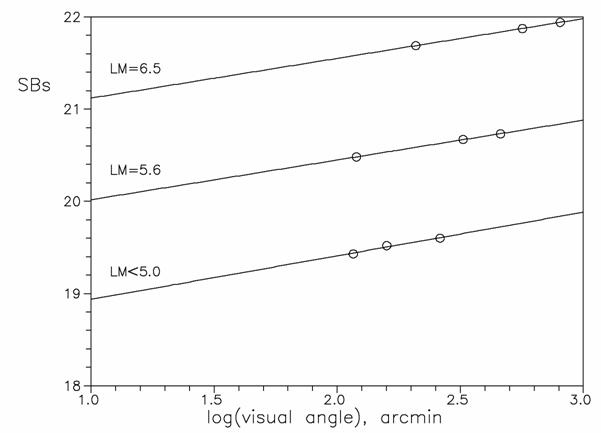
Figure 1 Faintest surface brightness (SBs)
visible through a 68 mm refractor on several background conditions. Data shown
were experimentally measured by the author defocusing stars of known magnitude.
The background surface brightness can be evaluated reading SB from the figure
at the critical visual angle (a value in the 6'‑10' range for the
background illumination conditions examined, that is a log value in 0.8-1.0
range).
In most cases, the background glows more even in rural
sites, reaching values often in the 21.5 to 22.5 mag΄arcsec2 range. Therefore, we
are unable to reach 7.8 magnitude stars at the naked eye, but quite more modest
values: 6.5 to 7.0. Going beyond 7.8 magnitude is only possible in laboratory
experiments, but there is a more exciting exception: using a telescope. With the
aid of a telescope, we make the background darker and we separate at greater
angular distances the disturbing stars, closing to those ideal conditions which
are required to reach the 8.5 LM. Of course, we'll not see stars of the
8.5 magnitude, but much more fainter ones due to the improvement in light
gathering made with the telescope. Closer to cities the situation becomes
harder: new emission lines appear as a result of artificial lights produced by
gas lamps, such as high pressure sodium or mercury, that strongly disturb us.
These lines can be eventually removed through interference filters.
The literature mentions an easy rule of thumb to
decide whether an object is visible or not. The idea is to establish a five per
cent of the sky's background brightness as a visibility threshold. Applying
that criterion, we would expect to see objects with a surface brightness up to
3.25 magnitudes above the background brightness:
|
|
(3) |
Suppose
a good sky, where 6.5 magnitude stars could be seen at the naked eye.
Substituting this value in Equation 2 yields 21.5 mag΄arcsec2 as the value of SB0.
A further substitution of SB0 in Equation 3 yields a
visibility threshold about 24.8 mag΄arcsec2.
Too simple to be really good. That criterion doesn't
take into account neither the telescope diameter nor the object's apparent
size, which are two very important factors. Given two objects having the same
surface brightness, the greatest one will result easier to be seen. This fact
is related with our vision system, which definitively is not a simple passive
light gatherer, as a photographic film. We don't observe with a telescope only:
we do it through our telescope, our eye(s), and our brain, which are associated
in order to process signals to produce meaningful data. In that way, as we
increase the object's apparent size varying magnification, both the object and
the background become darkened in the same amount. But, as we are enlarging the
image, more retinal cells are contributing to confirm the perception of faint
signals. With all that, a significant image enhancement is achieved although
less light is arriving to a given retinal cell. Always? Well, not exactly: the
improvement is only true below a critical magnification, where background and
object are too darkened to obtain any enhancement in perceptibility via
increasing the object's visual angular size. We can benefit of these properties
of our vision system to see faint objects.
We can illustrate this fact in a dramatic way: let's
calculate the surface brightness of an Airy's disk produced by a star just at
the threshold. Suppose we are using a 68 mm refractor, which shows stellar
images about 1.7 arcseconds in diameter. Under moderate seeing conditions these
images are clearly upon the visual limits constrained by a steady atmosphere.
This tiny instrument can reach stars a little fainter than the 13th magnitude,
seven magnitudes weaker than those values measured at the naked eye, but one
can read in many books that the TLM for this instrument should be the 11th
magnitude. Why this difference?
The telescopic limiting magnitudes (TLM)
published in the literature are certainly quite conservative. This deserves
some more comments. Traditionally, TLM values are calculated for a
background brightness similar to that visible at the naked eye. That is, when
the eyepiece used at the telescope presents the same exit pupil than the human
eye: 7.5 mm, so there is only a geometrical gain in light gathering. The
equation for traditional values of TLM is just based on the calculation
of telescope's aperture to eye's pupil surface ratio:
|
|
(4) |
where LM is the magnitude of the faintest star
visible at the naked eye, and DIAM is the telescope's aperture in
millimeters. Under such conditions the observer's vision capability is severely
restricted, and the telescope cannot develop its true power. For instance, a
11.3 TLM is obtained for a R68 telescope when 6.5 stars are visible at
the naked eye; too modest to be good.
Fortunately, the outlined situation is rarely found in
practice: through many eyepieces the sky background glows substantially less,
allowing us to see fainter stellar objects. As an example, in a common night
(6.5 LM), the mentioned 68 mm little refractor can easily show stars
fainter than 12.5 magnitude through a wide range of eyepieces. Let's consider
that when the magnification is ΄150, a R68 telescope is able to show 13.2 magnitude
stars in a 6.5 LM night. The surface brightness of an stellar source at
the threshold (13.2 magnitude, 1.7 arcseconds wide) would be then 14 mag΄arcsec2. At this point, I
recommend you to have a look to Table 1 again, to familiarize a bit more with
usual SB values for deep sky objects.
Table 1 Typical surface brightness values for astronomical
objects.
|
Object |
Size |
Visual
magnitude |
SB mag΄arcmin2 |
SB mag΄arcsec2 |
|
Sun |
32' |
26.8 |
19.5 |
10.6 |
|
Venus |
9.8" |
3.9 |
8.1 |
0.8 |
|
Full moon |
32' |
12.6 |
5.3 |
3.6 |
|
Jϊpiter |
45"΄42" |
2.5 |
3.2 |
5.4 |
|
Nautical twilight |
all sky |
meaningless |
5.0 |
14.0 |
|
Metropolitan site, LM=4.5 |
all sky |
meaningless |
7.0 |
16.0 |
|
Ring Nebula, M 57 |
86"΄62" |
8.8 |
9.0 |
17.9 |
|
Crab Nebula, M 1 |
6'΄4' |
8.4 |
11.6 |
20.5 |
|
Dark sky background, LM=6.5 |
all sky |
meaningless |
12.5 |
21.5 |
|
Helix Nebula, NGC 7293 |
12'΄10' |
7.3 |
12.2 |
21.1 |
|
M 51 main (NGC 4594) |
9'΄7'.5 |
8.4 |
12.7 |
21.6 |
|
M74 |
10'΄9'.6 |
9.2 |
13.9 |
22.8 |
|
Planetary nebula Abell 72 |
132"΄121" |
13.8 |
15.2 |
24.0 |
|
Rural site background, ML=7.5 |
all sky |
meaningless |
15.3 |
24.2 |
|
Sculptor Dwarf |
75' |
10.5 |
19.6 |
28.5 |
The reader should conclude that something is wrong,
since if the SB threshold actually is 14 mag΄arcsec2, we virtually should
expect to see no diffuse object!. No Messier object has such a high average
surface brightness. The Messier object having the highest SB, M57, is
only 18 mag΄arcsec2.
However, it can be verified that using this instrument, images presenting 22
mag΄arcsec2
are easily perceived, 1500 times fainter than the faintest stellar image we
are able to see. Even more: just changing the eyepieces to get optimum
magnifications, we'll see that this process can be carried out further, up to SB
above 24 mag΄arcsec2.
Therefore, we are forgetting to include something that is very essential in our
treatment. We will tackle later the problem of extended objects, but first
let's finish the discussion on the visibility of stellar objects (e.g.,
stars, smaller planetary nebulae, and farther galaxies with bright cores).
The true limiting stellar magnitude we can reach with
a given telescope (TLM), at a given magnification (MAG), when
stars of LM magnitude can be seen at the naked eye, is easily calculated
through the next two formulae sequentially substituted, that can be easily
obtained combining the concepts of darkening, surface ratio between telescope
and eye, and the polynomial approach for predicting background surface darkness
(Equation 2):
|
|
(5) |
|
|
(6) |
Equation
5 yields the background surface brightness as seen through the telescope, that
is, darkened by effect of magnification, whereas Equation 6 gives us the
faintest star visible at the eyepiece on that artificially darkened background.
There is a new variable in Equations 5 and 6, namely the transmission factor
(t), that represents the percentage of gathered light we benefit from.
The transmission factor takes into account not only light diminishes due to
central obstructions (secondary mirrors), glass absorption, undesired
reflections or light scattering, but also gains due to the experience level and
the ability of the observer. In this work, we will take t = 0.9 for
refractors and t = 0.7 for reflectors.
Since maximal TLM happens when the sky
background presents a 27 mag΄arcsec2 surface brightness, one can derive
an equation similar to traditional TLM from Equation 4, but this time
more realistic:
|
|
(7) |
The
magnification necessary to get this darkening (i.e., the magnification
that better help us to see stellar sources), can now be derived from Equation
5:
|
|
(8) |
As
mentioned, the above expressions are only valid for stellar or semi‑stellar
objects. But when an extended object is observed, the prediction of visibility
fails. For this kind of problem, it must be taken into account, moreover the
surface brightness of both the object and background, the object's size (or, if
it is round, its global magnitude, being two variables mathematically linked
through the definition of SB). Some years ago I successfully used
empirical calibrates obtained through a little refractor. Nevertheless, the
theory developed by Roger Clark has been proved to be more suitable, at least
in some cases.
Now we'll introduce the Roger Clark's method for
predicting the visibility of extended objects. An analogous method derived by
the author, that even seems more reliable, will be explained further.
The Clark's Method
In Visual
Astronomy of the Deep Sky, Roger Clark proposed a method for predicting the
visibility of non‑stellar objects at a given telescope, as well as to
calculate the optimal magnification. The method is based on a previous paper
due to Blackwell and published decades ago, where medical measurements on the
eye's performance for detecting glowing objects on differently illuminated
backgrounds, were tabulated. Clark transformed those data to plot a graphic
relating the object's contrast with the apparent angular size required to see
the object at the threshold, under different background illumination
conditions. We'll call Blackwell/Clark's surface to this plot (see
Figures 3 and 4; just have a look now, since both of them will be explained in
detail below).
Some very interesting concepts have been introduced in
VADS. Perhaps the most important one is the optimum magnified visual angle
(OMVA): the angular size which allows seeing an object under optimal conditions
according to the eye physiology. By intuition we know that deep sky objects can
be optimally seen through certain magnifications. Indeed, as we increase the
eyepiece power, many objects become easier to see. However, this is only true
up to a certain magnification, beyond which the image diminishes quickly than
the eye's performance improves. Based on the response surface mentioned above,
Roger Clark plotted a second graphic that allows a quick estimation of the OMVA
(see Figure 2), arguing that all the points in the Blackwell/Clark's surface
where the first derivative is 1 represent perceptibility maximums. Since all
these points draw a curve on the surface, the OMVA estimation can be expedited;
this is the aim of the mentioned second plot (Figure 2). Once the OMVA is
obtained for a given object and observational conditions, just dividing this
angle by the object's minor axis leads to the optimum detection magnification
(ODM).
Perhaps the reader should appreciate now an example to
understand better this theory. The calculation of Clark's ODM consists of an
iterative process. Let's illustrate it finding the ODM for NGC6166, using a 254
mm telescope (t = 0.7) in a night where 6.5 magnitude stars could be
seen at the naked eye. NGC6166, the main member of the galaxy cluster Abell
2199, is an huge cD galaxy, shining with 14.0 photographic magnitude (about
12.5 visual), and measuring 2'.2 ΄ 1'.7 at the telescope. Study carefully now Figure 2,
whereas you are reading the following explanations, to understand how the
algorithm works. Two initial parameters are required: the object's minor axis (b
= 1'.7) and the sky's background surface brightness at the naked eye (SB0
= 21.51, obtained with Equation 2 for LM = 6.5). The
algorithm starts assuming an arbitrary initial magnification (MAG0 =
΄100), from which the
darkening is calculated (= +2.74, see Table 2, Note 1). Darkening is now
added to SB0 to obtain the background surface brightness as
seen through the telescope: SB01 (= 24.25), and we should
locate that value on the X-axis. From this darkened background (SB01),
a value for an optimal angular size (Ang1 = 73.8) is measured from
the projection on the Y-axis of the point located on the OMVA curve having the SB01
value previously calculated. Dividing Ang1 by the object's minor
axis, b, a new value of magnification is obtained (MAG1 =
73.8/1.7 = ΄43.1),
usually different from the previous value (MAG0 = ΄100). If MAG1 does not
fit with MAG0, the full process is subsequently repeated,
using the MAG1 value just obtained as the new initial
magnification at the current iteration.
The process is repeated as many times as required up
to obtain no significant difference between MAGi and MAGi+1,
that is, between two consecutive iterations. When this happens, we have ODM = MAGi
= MAGi+1. In the case studied, ODM is ΄37. Finally, we check whether the
object is visible or not, interpolating in the Blackwell/Clark's surface; we will
consider later how is this done. In the example, NGC6166 is actually visible
using the optimal magnification found (΄37).
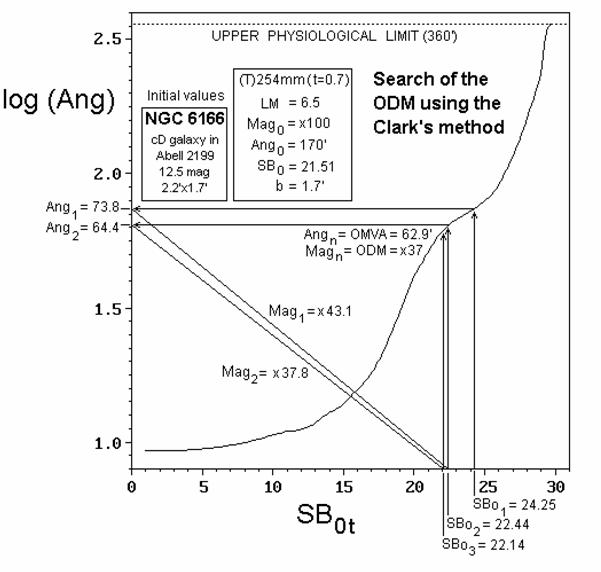
Figure 2 Calculation of the optimum magnification
for NGC6166 (12.5m, 2'.2 ΄ 1'.7) using the Clark's iterative algorithm described
in the text. This simulation corresponds to a hypothetical night at which 6.5
magnitude stars could be seen at the naked eye, using a 254 mm telescope with a
transmission factor t = 0.7. Apparent background values of surface brightness
SB0i at each iteration step are calculated via expressions (1) and
(2) shown in Table 2. The optimum detection magnification (ODM) is ΄37, according to this method.
Reasonable results are obtained in many cases. But,
surprisingly, if the method is applied to predict the visibility for objects
which are both bright but very small, it leads to inconsistent values. To
illustrate it, let's consider a little planetary nebula 2" wide and
shining with the 12.5 magnitude. Through a 254 mm reflector (t = 0.7) in
a 6.3 LM night, experience and common sense tell us that it should be an
easy object, since it's almost a stellar source and we should be able to see
stars three magnitudes fainter. To avoid a too large image, which could be even
greater than the rods area of our retina, we'll impose a six degrees constraint
on the object's apparent size for limiting possible magnifications.
Nevertheless, if we apply the Clark's Method, we conclude that ΄10800 is the optimum magnification!. The
object, in fact, was perfectly visible at a smaller magnification, but we have
enlarged it so much that it can not be perceived at all. Some tricks can be
proposed to avoid a so large magnification, but, in any case, the visibility
cannot be guaranteed at the end of the calculation process.
Such kind of result introduces severe doubts over the
procedure used to calculate the optimum magnification. The Clark's Method seems
predict useless magnifications when we want to see very small objects or almost
stellar sources, such as planetary nebulae or small galaxies. And, which is
more important, the results do not agree with those obtained when we predict
the visibility of stars of similar magnitude, that seem to be completely
reliable.
Equations 5 and 6 predict for instance that using a
254 mm telescope in a LM = 6.3 night, we are able to see stellar objects
shining with 12.5 magnitude from to ΄14. The maximum visibility will happen when the
background is darkened up to 27 mag΄arcsec2; that is over ΄390 (Equation 8). One should expect a
smooth transition between both procedures (i.e., Clark's Method and
Stellar Method, that is, Equations 5, 6, 7 and 8) as the object's size
increases, with a certain range of coexistence: an interval where nearly
identical predictions should be obtained with both methods. But that does not
happen.
The Threshold
Method:
an alternative approach for searching the
optimal magnification
Clarks
Method performs only an angular optimization, not considering the
objects visibility until the end of the calculation. It is quite surprising to
separate angular optimization from visibility optimization in an algorithm
designed for predicting the visibility, since we certainly want to find
magnifications where the object could be seen!. According to Roger Clark, the
optimum magnification is obtained considering only the objects apparent
dimensions. If an easy object is not visible at the Clarks ODM, perhaps we
require to define another kind of optimal magnification that balances
perceptibility with apparent angular size. We need to introduce ourselves
deeper into the visibility concept.
At this point it's convenient to take a few time
explaining the Blackwell/Clark's surface (see Figures 3 and 4), which, as
commented, gives the critical circumstances for observing any kind of object at
the threshold. This figure is extremely important, and you must spend some time
to understand it properly.
The Blackwell/Clark's graphic shows thus a
three-dimensional response surface seen from above, plotting the lost dimension
(height, Z-axis) on the X-Y plane as some contour lines. Only two axes are thus
conserved:
1.
The X‑axis is the object's apparent angular diameter (minor axis
multiplied by magnification): the object's size as seen through the eyepiece.
2.
The Y‑axis is the object's contrast, which we'll define right now.
In both X and Y axes, logarithms are used to extend
the linear behavior as possible. The Z‑axis, which is lost due to the
projection, is the background surface brightness required for perceiving at the
threshold an object with a given size (X‑axis) and surface brightness (Y‑axis).
Several lines have been overlaid, each one corresponding to a given background
surface brightness, in the range from 4 to 27 mag΄arcsec2. In this way, if an
object with a certain apparent size were projected on a background of a certain
surface brightness, this graphic would yield the critical surface brightness
beyond which the object would be visible.
The Y-axis involves a new concept, called contrast:
the object‑to‑background surface brightness ratio, given by:
|
|
(9) |
When the logarithm of C is taken,
units are obtained that grow at the same rate that the visual stimulus. This is
just the Fechner's Law, a well-known rule for any deep-sky or
variable-star observer, which justifies the relation between magnitudes and
visual stimulus. Contrast tells us how faint an object should be in order to be
visible at the threshold, taken as zero the background brightness. Or, if you
prefer, contrast allows the calculation of the limiting surface brightness we
can reach: SBlim = SB0 2.5 log C.
Let's suppose a given object observed at certain sky
conditions. We can calculate the limiting surface brightness (SBlim)
at several magnifications. When we plot the results on the Blackwell/Clark's
surface, a curve results that we'll call limit of detection. For the
Clark's Method to work, minimums for all possible limit of detection curves
should be located always over the OMVA curve. Surprisingly, this fact does not
seem to occur.
Plotting a limit of detection curve is not so hard,
since we can easily calculate for each magnification, the logarithm of the
object's apparent size (X) and the darkened background surface brightness
as seen through the telescope at that magnification (Z):
|
|
(10) |
|
|
(11) |
In
Equation 10, b is the length of the object's minor axis measured in
arcminutes. The minor axis is used instead of the major dimension for the
reason that the former is actually the limiting factor when observing a faint
image. The above expressions give us the coordinates Z (darkened
background) and X (apparent size). The third coordinate (i.e.,
the Y-axis, or logarithm of contrast), should be evaluated from those (Z
and X) values using the corresponding contour line.
As commented, the minimum visible contrast for the
considered object at a certain magnification is represented by the Y‑axis,
whose coordinates are interpolated from the Blackwell/Clark's graphic starting
from X and Z values. When successive points (each one
corresponding to a different magnification) are plotted together and joined, a
curve is obtained: the above introduced limit of detection. The minimum
of that curve yields the angular size which allows to gather the faintest
possible surface brightness in the studied object. Dividing the so‑calculated
angular size by the object's minor axis, the optimum magnification according to
both visibility and apparent angular size is obtained. We'll call it OptDM to
emphasize that it is a different concept to Clark's ODM.
Numerically speaking, a risk arises when working with
stellar sources: if zero is used for the object's apparent size, log(0) and
divisions by zero will appear. To avoid it, the diameter of the Airy's disk
produced by the telescope should be used. In fact, that is what we actually see
for a really small object.
It should be pointed out that at increasing
magnifications, despite of the fact that both the object and the background are
darkened, the ratio between SB and SB0 remains
constant: the logarithm of the object's contrast does not depend on
magnification. That's why the graphical representation of the object's contrast
is just a straight line, that we'll call object contrast line. Do not
confuse this concept with the smaller visible contrast represented by the limit
of detection, that actually depends on magnification.
For deciding the condition range where the object is
visible, we need to plot two lines overlaid on the Blackwell/Clark's graphic:
(1) the limit of detection curve, and (2) the object's contrast line. If the
limit of detection (Equations 10 and 11) is completely located above the
object's contrast line, then we can conclude that the object will not be
visible at any magnification. For the object to be seen, the limit of detection
should be located below the object's contrast line for the whole range of
available magnifications, or at least for some portion of it. The magnification
corresponding to the maximum of visibility will be located at the point where a
maximum distance exists between the object's contrast line and the limit of
detection, as far as the object is visible, of course.
At this point, an example will help you to understand
the full process. The considered object will be again NGC6166, as in the
Clark's example (2'.3 ΄ 1'.7, 12.5 visual magnitude). We will take a 254 mm
reflector (t = 0.7) as the working instrument, and the naked‑eye
limiting magnitude will be also LM = 6.5 (SB0 = 21.44,
see Equation 2). Experience tells us that no difficulty should arise in this
observation. All the algorithm is explained in detail in Table 2.
With values from the last column of Table 2 we can
introduce three new observational parameters:
OptDM/OptDA Optimum
detection magnification/angle, at which the object can be seen under the most
favorable conditions, accessing to faintest details or, what is equivalent,
more similar to the background (smaller contrasts). In Figure 3, we can see
that OptDM corresponds to the minimum of each limit of detection plotted, and
that these points are not generally located on the OMVA curve. In the example
of Table 2, OptDM is slightly greater than ΄50. ODM, as calculated with the Clark's
procedure, results ΄40.
OptDM, as well as OMVA ODM, tend to be similar in magnitude for objects having
appreciable dimensions, what explains why Clark's OMVA works in many cases.
MaxDM/MaxDA Maximum detection magnification/angle, at which the object's apparent dimensions
have been enlarged up to coincide with the limit of detection. If the object
has internal details, they will be easier to detect under these conditions.
This parameter corresponds to the crossing between the object's contrast line
and the limit of detection. Due to the horizontal expansion in the X-axis
(logarithmic scale), the values for this parameter are relatively uncertain, so
they should be taken with care. In Table 2, MaxDM is about ΄250, a value fully concordant with the
experience.
MinDM/MinDA It can be defined also, although of smaller
interest, a minimum detection magnification/angle. It's no more than the
minimum magnification required to just start seeing the object. In this work,
MinDM has been considered at least DIAM/7.5, to avoid losses of light
gathering by using too low powers exit pupils must be smaller than 7.5 mm for
all cases. For weak and small objects, MinDM is greater than DIAM/7.5.
Table 2 Visibility of NGC 6166 (2.2' x1.7', 12.5m) in
a 6.5 LM night, using a 254 mm telescope. The process of building a
threshold curve is step by step given.
|
Instrument
(T)254, t = 0.7 Object's size and visual
magnitude
2'.2΄1'.7, 12.5m Object's surface
brightness
SB = 22.56 mag΄arcsec2 Limiting magnitude at the naked
eye
LM = 6.5 Background surface
brightness
SB0 = 21.44 mag΄arcsec2 Object's contrast
line
Y = log C0 = 0.4 (22.56 21.44) = 0.45 |
||||||
|
Magnification |
Darkening *1 |
SB0app *2 |
log(axis) *3 |
log C *4 |
SBlim *5 |
log(C0/C) *6 |
|
40 |
0.75 |
22.18 |
1.83 |
0.62 |
22.98 |
+0.17 |
|
50 |
1.23 |
22.67 |
1.93 |
0.63 |
23.01 |
+0.18 |
|
60, optimum |
1.63 |
23.07 |
2.01 |
0.63 |
23.02 |
+0.18 |
|
70 |
1.96 |
23.40 |
2.08 |
0.63 |
23.01 |
+0.18 |
|
80 |
2.25 |
23.69 |
2.13 |
0.62 |
22.99 |
+0.17 |
|
90 |
2.51 |
23.95 |
2.18 |
0.62 |
22.97 |
+0.17 |
|
120 |
3.13 |
24.57 |
2.31 |
0.58 |
22.88 |
+0.13 |
|
150 |
3.62 |
25.05 |
2.41 |
0.53 |
22.77 |
+0.08 |
|
180 |
4.01 |
25.45 |
2.49 |
0.50 |
22.67 |
+0.05 |
|
250, not visible |
4.73 |
26.16 |
2.63 |
0.41 |
22.45 |
0.04 |
|
300, not visible |
5.12 |
26.56 |
2.71 |
0.33 |
22.26 |
0.12 |
|
400, not visible |
5.75 |
27.18 |
2.83 |
0.15 |
21.80 |
0.30 |
|
500, not visible |
6.23 |
27.67 |
2.93 |
+0.08 |
21.23 |
0.53 |
|
*1 Darkening = 5 log ( 0.1116 ΄ DIAM / MAG), where DIAM is the
telescope diameter in mm, and MAG is the magnification. *2 Apparent background surface brightness, as is seen
through the eyepiece: *3 Logarithm of the apparent minor axis (as seen
magnified with the telescope), in arc-minutes. Thus, for NGC6166, whose minor
axis is 1'.7, log(axis) = log(1.7 MAG). *4 Obtained interpolating from Blackwell/Clark's
surface (Figures 3, 4) the values of SB0app and the
logarithm of the magnified minor axis. *5 Minimum surface brightness that can be detected in
a 254 mm telescope using the current magnification SBlim = SB0
2.5 log C. *6 Visibility, from which the object's contrast has
been subtracted: Visibility = Y logC. The object can be seen
if this value is greater than zero. The greater this value, the easier to see
the object. |
||||||
Drawing the limit of detection we should plot the
points of columns 3 (X-axis) and 6 (Y-axis) of Table 2 on the Blackwell/Clark's
surface. It should be remarked again that using the Blackwell/Clark's surface,
both size and visibility are simultaneously optimized: angular optimization is
unnecessary, since it is implicitly included in the Blackwell/Clark's
surface.
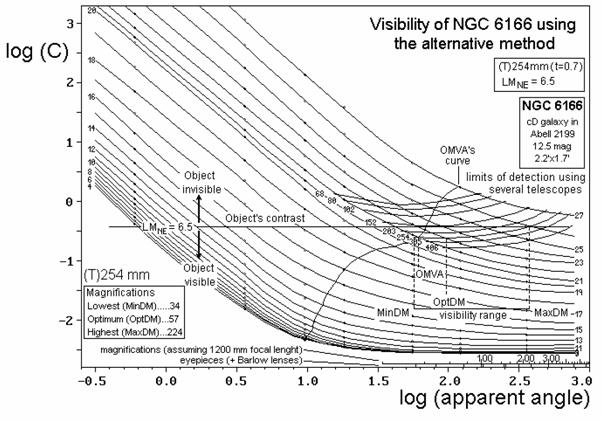
Figure 3 Calculation of the optimum detection
magnification for NGC6166, according to the Threshold Method explained in the
text and illustrated in Table 2, using the same conditions than those for
Figure 2. The minimum magnification required to see this galaxy (MinDM) is that
necessary to obtain a 7.5 mm exit pupil, that is, 254/7.5 = ΄34. From this value, one can increase
telescope's power up to arriving to a visibility maximum. That is the optimum
detection magnification (OptDM), which is ΄57 for a 254 mm telescope. The galaxy
could be seen at progressively higher power, up to a magnification at which it
is confounded with the background: the maximum detection magnification (MaxDM),
΄224 in this case. The visibility curves corresponding to different
apertures are overlaid on the same graphic. It's easy to realize that smaller
optimum detection magnifications are obtained for smaller telescopes. However,
smaller telescopes also require smaller exit pupils. All these results
contradict the Clark's theory, but fits better with the user experience on
deep-sky. Thus, for telescopes with apertures of 68, 80, 102, 152, 203, 305 and
406 mm, the optimum magnification increases: 32, 33, 37, 48, 52, 61 and 67,
respectively, whereas the exit pupil also increases: 2.1, 2.4, 2.8, 3.2, 3.9, 5.0
and 5.7 mm, respectively.
An observer can design a working
strategy based on the parameters we have just defined. MinDM will lead to the
minimum useful magnification. OptDM will give the most suitable one in order to
detect the whole object. Magnifications higher than OptDM, but near to MaxDM,
will be useful to distinguish internal details. The evolution of the limit of
detection, by the other hand, will show how critical the optimum found will be,
letting us to know in advance how much we can depart from OptDM without
important losses of performance.
In the Clark's Method the object is assumed to be optimally
visible at the OMVA. Clark states that the OMVA curve is obtained from the
Blackwell/Clark's plot, joining all those points where slope is equal to 1.
Perhaps that's true, but only for a given object observed with a specific
telescope under some particular sky conditions. The minima of the limits of
detection are actually due to some irregular spacing existing between the
Blackwell/Clark's contour lines, so there is no reason for them to be located
at the points where the first derivatives are 1. This fact can be illustrated
(Figure 3) through the same example we saw referring to the Clark's Method:
NGC6166. Figure 3 also shows limits of detection corresponding to several
telescopes, calculated via the Threshold Method. As can be easily seen, only
the curve for one telescope (approximately 125 mm, not drawn) would present its
minimum located just on the OMVA curve. Consequently, although the Clark's
optimum magnified visual angle (OMVA) has a defined position on the
Blackwell/Clark's surface, there is no reason to think that this line will
contain all the points of maximum visibility under all conditions.
What would happen with the hypothetical planetary
nebula (2" sized, 12.5 magnitude, (T)254, LM = 6.3) introduced in
the Clark's Method, if treated with the Threshold Method? We find that this
nebula is visible at any reasonable magnification (see Figure 4), but there is
a maximum of perceptibility at ΄310 (OptDM) with a visibility of +1.2, in a point far
away from the OMVA curve. Under good conditions, the object could be observed
even at ΄1000
of more, a circumstance that would permit to observe eventual internal details,
increasing the magnification as far as the atmosphere allows us. This coincides
with the predictions made via the stellar method and, what is more important,
fits better with what an expert deep‑sky observer would may expect.
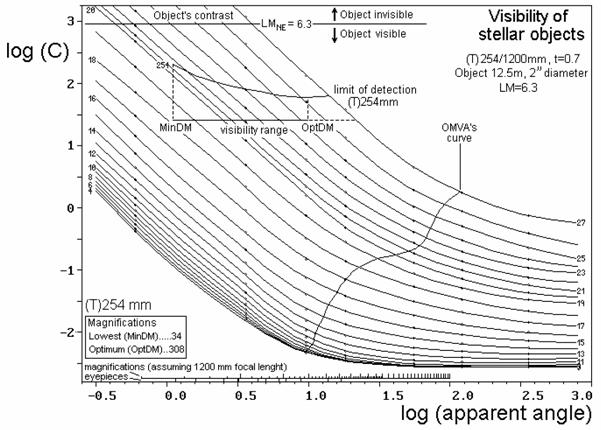
Figure 4 Detection of a stellar object (2"
diameter, 12.5 visual magnitude), through a 254 mm telescope (t = 0.7), when
6.3 magnitude stars could be seen at the naked eye. With the Threshold Method,
the prediction points that the object is visible at any reasonable
magnification, but optimally at ΄308. Clark's Method predicts an optimum
magnification at ΄10800. At such a high power, however, the object is
not visible. The stellar method predicts a maximum visibility using ΄390 (see text), which is fully congruent
with the Threshold Method: ΄390 is the limit of detection corresponding to a SB0
= 27 mag΄arcsec2; as the object studied is not
punctual, but little extended, the optimum magnification is somewhat smaller: ΄308.
Main Conclusions
1. With the
Threshold Method, higher magnifications are not necessarily predicted for
smaller telescopes to see a given object. Instead of that, smaller
exit pupils are predicted for smaller telescopes. A smaller telescope must make a proportionally
greater effort in order to see a given object. That means that smaller
telescopes need to darken the sky's background more with the purpose of
outstanding better the object. However, the smaller the exit pupil, the harder
to see the object.
2. Another result
that agrees with common sense: smaller exit pupils are also predicted
for bad sky conditions.
3. Although
optimal values of contrast are predicted, there is no reason for they to lay on
the Clark's OMVA curve.
Differences are specially significant for small objects.
4. The position
and shape of the limits of detection depend on the sky's background surface brightness.
These curves do not lay in a permanent position on the Blackwell/Clark's
surface, as they are also a function of the limiting magnitude; Clark's Method underlay on the idea
that they are independent.
5. The Threshold
Method is fully congruent with predictions of visibility for
stellar or nearly stellar objects. Modifying Equation 2, which gives the limiting magnitude, visibility
can be successfully predicted even for stars under twilight conditions.
Some Considerations on Real Deep-Sky
Objects
Due
to the fact that real object's images are simplified as elliptical homogeneous
glows, inner light‑distribution variations may lead to different results
to those expected. In this way, a Sc galaxy seen from above usually results
harder to see than an elliptical one, with a more outstanding core. A faint,
high-gradient globular cluster is easily seen, whereas a brighter, but with a
flatter light profile globular cluster as often happens with Palomar
clusters, will result harder to see. Observers take into account these factors
in order to enhance their evaluations of visibility. Identically, one should
consider these non-idealities in numerical approaches, to judge prediction
adequately. That is, the corrections in the visibility prediction when we cross
the line from an ideal object to a real deep-sky object. Parameters as the
Hubble or Vacouleurs type for a galaxy, or the Shapley gradient class for a
globular cluster, should be considered as correctors to adapt predictions to
reality, but anyway, mean object brightness, size and background brightness are
indeed the most essential features. Obviously, the more even the object, the
more adequate the prediction. Although an homogeneous distribution of light has
been assumed and this is not true for real deep‑sky objects, observation
of internal details, as have been mentioned, will be favored if we use
magnifications between OptDM and MaxDM. For some cases, it can occur that even
magnifications higher than MaxDM allow to see better small parts of the object.
Another important factor to be taken into account
relates to the data used for predictions. Magnitude and size entries differ
significantly among catalogues. What catalogue should be the best? In many of
them, compiled data correspond to extrapolations in the object's light profile,
which is technically correct, but not useful for our purposes, since we'll
never arrive to see those regions in the object. In other catalogues data
correspond to photographic measures. Crossing data helps us to validate them,
discarding some sources and averaging others. I prefer to use, when available,
visual observations of qualified observers as magnitude and size sources,
because those values use to be closer to standard images than extrapolated
measurements. Anyway, one should take into account the variability of data
sources to estimate the confidence of the predictions. An optimist and
fatalistic pair size-magnitude can help us to bracket our predictions and yield
a more accurate estimation of our possibilities to see the object using our
telescope.
For
field work, I prepared a set of special graphics that reduces all the results
of the Threshold Method for some usual telescopes. One only needs to get the
corresponding graphic for his/her telescope, to know the magnitude, size and
surface brightness of the object he/she wants to see, and that's all. No
calculation required!
Figure 5 is given as an example: this is a universal
graphic to predict the visibility, and to calculate the OptDM, for a 254 mm
reflector under LM greater than 5.5. Worth information can be obtained
from the plot:
1. For a given object, the process starts
locating the size (length of the smaller axis) on the graphic's X‑axis.
Next, we find the minimum surface brightness, SBlim (A‑scale,
and associated "A" curves). This is done by plotting a vertical
straight line from the X‑axis up to intersect the "A" curve
corresponding to the limiting magnitude perceptible at the naked eye, and then
a second, perpendicular straight line from this point to the left, up to
crossing the A‑axis. If the object's surface brightness (Equation 1) is
smaller than the SBlim value just obtained, then the object
will be visible.
2. For near‑circular objects, visibility
can be predicted without needing to calculate its surface brightness, by using
the B‑scale and associated "B" curves, in a similar procedure
to that just explained: after finding the object's minor axis on the X‑axis,
a vertical line is plotted up to intersect the "B" curve
corresponding to the current limiting magnitude at the naked eye. Then, a
second line plotted from that intersection to the right, up to crossing the
B-Axis, where the telescopic limiting magnitude (TLM) can be read. If
the object's magnitude is smaller than the obtained value, it will be
visible.
3. Finally, the same graphic and procedure can be
repeated to find out the optimum detection magnification. Now the C‑axis
and associated "C" curves should be used, following an analogous
procedure to that one explained above for A and B curves. However, some
additional comments deserve to be pointed out, especially the reason for those
odd and flat regions in the curves. Why does it happen?. The explanation is
somewhat complex since several factors concur into it. The first consideration
is that limits of detection can be nearly flat and the calculation of the
optimum detection magnification is therefore not very accurate. The second one
is that Blackwell/Clark's surface presents regions with varying accuracy level;
those regions with smaller slope lead to limits of detection poorly defined,
which happens for objects with noticeable dimensions. Finally, when we examine
a collection of images presenting all the same surface brightness but an
increasing size, the way they are perceived suddenly changes: up to a given
point the object becomes too easy to see, and we should use the minimum
magnification, the magnification that most concentrates the light. This
produces a sudden drop. Immediately below that magnification, the limit of
detection is flat and no improvement is achieve increasing the eyepiece power.
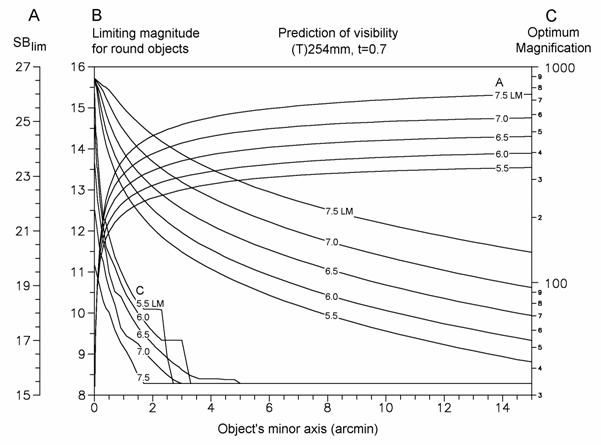
Figure 5 An example of universal graphic
constructed for a 254 mm telescope (t = 0.6), that can be used for predicting
the visibility of astronomical objects as well as to evaluate their optimum
magnification.
The
author would be very interested in knowing the opinions of those who decide to
use the Threshold Method. It is not too hard to write a computer program that
can perform all the calculation process in a quick and efficient way. For
instance, all the figures presented in this work have been generated through a
computer program that was written by the author, which can operate with the
Clark's Method and the Threshold Method as well. At least according to my
experience in practical astronomy, results obtained until now with the
Threshold Method seem to be correct and reliable.