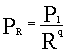
|
|
|
|
Verificación de la ley Rango-Tamaño en los municipios del
A.M.V.
Para cuantificar las relaciones internas de los sistemas de ciudades , se utilizan distintos indicadores , que se basan en relaciones , que con mayor o menor aproximación verifican todos los sistemas de ciudades
Una de estas relaciones es la llamada ley Rango-Tamaño (rank-size) . Esta antigua ley establece que el tamaño (medido por su población) , PR de un municipio de rango R (ordenados los municipios de mayor a menor)
verifica que :
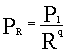
Donde P1 es la población del municipio mayor (mayor población , en nuestro caso Valencia) y q es un coeficiente a determinar.
La regularidad de esta ley ha sido contrastada para sistemas nacionales y regionales de ciudades que se caracterizan por un alto nivel de urbanización , una gran extensión , o una tradición histórica consolidada de asentamiento urbano . En cambio , cuando existe un gran desequilibrio entre la ciudad mayor y el resto o cuando no existe propiamente una entidad de población dominante sobre las demás , la ley se cumple de una manera vaga , o sencillamente no se verifica en absoluto.
La verificación de la ley apunta , por lo tanto a una estructura equilibrada de asentamientos urbanos según su tamaño poblacional y sugiere la existencia de una compleja red de relaciones que mantiene las dimensiones urbanas del territorio armónicamente jerarquizadas. En cambio la verificación de la ley da a entender un sistema de relaciones entre los entes poblacionales que tiene una escasa importancia y un notable desequilibrio del reparto de la población.
Para verificar el comportamiento del Área Metropolitana de Valencia respecto a esta ley se ha estimado por regresión mínimo cuadrática la relación tras , claro está , linealizarla.
Así : la
relación original es como ya se ha planteado .
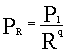
Linealizándola tomando logaritmos sería :
![]()
Y a
partir de esta nueva función estimar la regresión entre
![]() y log (R)
y log (R)
En base a los datos de población de los municipios del año 2001 , y ordenados éstos como ya se apuntó.
El modelo resultó .
![]() con coeficiente de correlación
de 0,928 .
con coeficiente de correlación
de 0,928 .
Podemos interpretar los resultados comparando con los resultados obtenidos para otras agrupaciones de municipios y ciudades .(fuente)
| SISTEMA DE CIUDADES | MODELO | COEF. DE CORRELACIÓN |
| CIUDADES DEL MUNDO CON MÁS DE 100.000 HB | LOG(P)=15,17-0,406LOG(R) | 0,6843 |
|
CIUDADES DEL MUNDO CON MÁS DE 2,5 MILLONES DE HB |
LOG(P)=16,93-0,551LOG(R) | 0,9764 |
| CIUDADES ESPAÑOLAS CON MÁS DE 40.000 HB | LOG(P)=16,04-1,2503LOG(R) | 0,9687 |
| ÁREA METROPOLITANA DE VALENCIA | LOG(P)=12,823-1,173LOG(R) | 0,928 |
Vemos que el grado de verificación de la ley es muy alto lo que nos indica que la jerarquización de los municipios del A.M.V en cuanto a población en el año 2001 es muy adecuada. Lo que se contrasta con los buenos resultados que se observan si comparamos la población real de cada municipio con la teórica de jerarquización óptima.
La ley Rango-Tamaño es también conocida como la
ley
de Zipf. La ley Rango Tamaño fue postulada por
Lotka en
1925 pudiéndose hablar de que la ley de Zipf es un caso particular de ésta ,
un caso , en el que se plantea que el parámetro q toma el valor 1,
estudiándose las desviaciones de las estimaciones respecto a dicho valor.
Ir a
análisis de cumplimiento de la ley de Zipf en el A.M.V.
Se comprueba también la jerarquización de los municipios con el estudio de la concentración de la población , tanto teórica , como real para el año 2001 .

