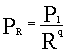
|
|
|
|
LA LEY DE ZIPF EN EL ÁREA METROPOLITANA DE VALENCIA
La ley de Zipf puede considerarse como un caso particular de la conocida ley de Rango Tamaño , propuesta por Lotka . La aportación de Zipf a la ley Rango-Tamaño radica en la peculiaridad de plantear que el valor del parámetro p ha de valer uno cuando exista una perfecta jerarquización de las ciudades o municipios que componen o forman parte de un determinado espacio.
La ley rango tamaño establece que el tamaño (medido por su población) , PR de un municipio de rango R (ordenados los municipios de mayor a menor)
verifica que :
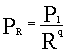
Donde P1 es la población del municipio mayor (mayor población , en nuestro caso Valencia) y q es un coeficiente a determinar.Como se ha dicho la ley de Zipf establece que dicho coeficiente ha de ser 1.
De cumplirse la ley de Zipf la ciudad más grande de un grupo estudiado será k veces mayor que la k-esíma , ordenadas las ciudades o municipios de mayor a menor.
Cuando q > 1 la ciudad de más población es mayor de lo que le corresponde, por lo que tenemos una mayor desigualdad entre las ciudades y municipios, y la mayor ejerce un poder excesivo de dominación sobre el resto.
Cuando 0<q<1 la pendiente de la curva es menor que la predicción de Zipf , existe un distribución más homogénea del tamaño en población de los municipios. Sin embargo , si el valor de q < 0,7 el grado de dispersión es excesivo.
Según Berry (1961) la distribución Rango-Tamaño , y por tanto su desarrollo en la ley de Zipf es el resultado de procesos de desarrollo estocásticos de los lugares próximos .Partiendo de que las distribuciones logonormales son casos límite de los procesos de crecimiento estocástico (Simon, J(1955)) , se plantea que la existencia de distribuciones logonormales implica la aparición de entropía .
Derivándose dos ideas del planteamiento de Berry :
a) Las distribuciones espaciales logonormales
prevalecen en procesos de crecimiento estocástico y hacen aumentar la entropía.
b) las distribuciones "apuntadas" (mayor curtosis) prevelecen siempre que los
procesos estocásticos de crecimiento se vean afectados por algún factor
sistemático que aumente la información.
Por tanto , mayor entropía implica una distribución más
regular de las ciudades , mientras que menor entropía (información creciente)
conduce a una distribución de ciudades concentrada , próxima en estructura
a la que plantea la teoría del lugar central de Christaller.
Si como plantea Berry , la entropía aumenta con el tamaño del país , la renta , y la mejora en las estructuras políticas y administrativas .Se puede plantear que este aumento de la entropía traerá consigo una distribución más regular de las ciudades cuya expresión máxima y límite será el cumplimiento de la ley de Zipf.
Se ha planteado este cumplimiento de la ley de Zipf , para los municipios que componen el Área Metropolitana de Valencia , llegándose a los siguientes resultados.

