o bien:
|
|
|
|
EL MODELO DE DIFUSIÓN CON LA DISTANCIA EN EL SUPUESTO DE
ISOTROPÍA DEL ESPACIO METROPOLITANO.
Caso de una sola característica metropolitana
Asumiendo el decrecimiento exponencial desde el lugar central de las características metropolitanas, el caso más simple a considerar, es aquél en el que consideramos que el espacio es isótropo respecto de la característica estudiada.
En ese caso, los valores de la variable considerada se comportarían de acuerdo a una función del siguiente tipo
o bien:
considerando las
coordenadas cartesianas x ,y (con r2=x2+y2,
y g(x,y)=f(r(x,y)) en donde
0 es el valor de la variable en el lugar central y
f(r) es una función positiva y creciente
r,
y g(x,y) presenta simetría circular.
El caso más
elemental es por lo tanto:
o bien
representado en la figura siguiente:
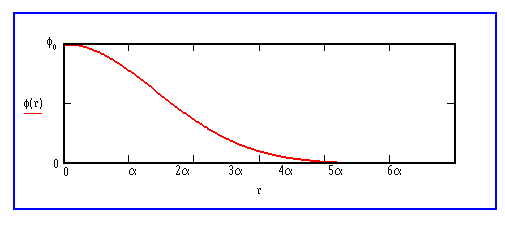
En
una situación tan restringida como la anterior, las isopletas ,
k (x,y,C),
correspondientes a cada valor constante de ,
(x,y)=C vendrían dadas por la
expresión:
x,y
k (x,y,C)
x2+y2=
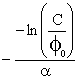
que son, obviamente, isopletas circulares:
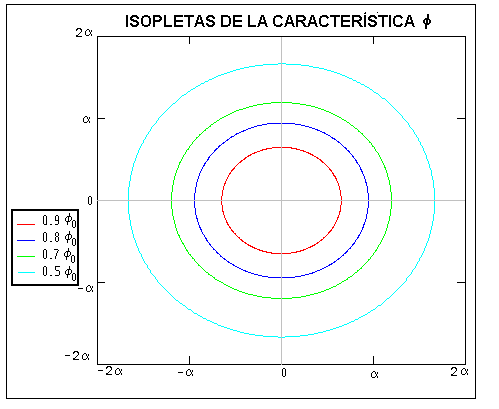
Por
otro lado la simetría circular de un modelo como éste nos permite obtener la "pared
metropolitana" de la característica estudiada con mucha facilidad, ya que estará
constituída por la circunferencia de radio r0, donde r0 será el
valor que anule la segunda derivada de
(r):
''(r)=(4α2r2-2α).(r)= 0
r0 =
Por
último, el modelo sería muy fácil de estimar por regresión, a partir de datos
empíricos, simplemente tomando logaritmos:
lo que supone un modelo lineal entre
y
r2 .
