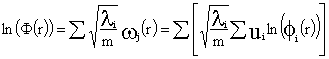EL MODELO DE DIFUSIÓN CON LA DISTANCIA EN EL SUPUESTO DE ISOTROPÍA DEL ESPACIO METROPOLITANO.

Caso de más de una característica metropolitana

    Lo expuesto hasta aquí, considera una única variable, , como indicadora de la metropolitaneidad. Sin embargo, la metropolitaneidad no es una magnitud directamente observable, sino una característica que sólo resulta parcialmente " explicada " a través de una serie de variables socioeconómicas que nos informan por separado sólo de algunos rasgos propios, tales como la aglomeración residencial, la terciarización, la concentración espacial de los flujos de transporte, del empleo de los centros de decisión, etc.

    Por tanto, y supuesto que se hayan considerado todas las variables relevantes, la metropolitaneidad debería expresarse como un indicador que considerara conjuntamente el efecto de todas ellas:

    Un indicador conjunto plausible debería ser reproductivo con respecto al modelo considerado; esto es, debería tener una distribución espacial decreciente exponencialmente con el cuadrado de la distancia.

    En este sentido, un indicador global que mantuviera esta esquema de variación podemos encontrarlo tomando una media geométrica ponderada de las variables :

donde las ponderaciones

nos darán cuenta de la contribución de cada característica     al indicador global,     .

    Obviamente, la variación con la distancia de este indicador global de metropolitaneidad será:

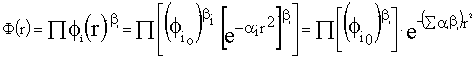
donde:          

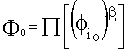
siendo             

    Reproduciendo, por lo tanto, el mismo tipo de variación: un modelo fácil de estimar y analizar según los esquemas anteriores, tomando logaritmos:              

    En el que el logaritmo de nuestro indicador sería, la media aritmética ponderada de los logaritmos de las características estudiadas:                

    Así pues, el problema de considerar un indicador general de metropolitaneidad se transforma en el de encontrar unas adecuadas ponderaciones para cada una de las características consideradas.
    Una estrategia plausible para ello es considerar como indicador general la media ponderada de las componentes principales de las variables   ponderadas por las raíces cuadradas de los correspondientes valores propios (Sanz,E, et. al.;1982),para de esta manera considerar la contribución de cada característica proporcional al efecto que tiene en la variabilidad total del conjunto de los datos:

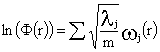
dondees la j-ésima componente principal:      

siendo las u_j las correspondientes ponderaciones factoriales y donde las son los correspondientes valores propios de cada componente principal:      

?