EL MODELO ANISÓTROPO DE DIFUSIÓN CON LA DISTANCIA.

 Planteamiento y discusión del M.A.D.D.

        Hasta ahora hemos supuesto que el espacio metropolitano era isótropo y no presentaba direcciones privilegiadas ,en ningún sentido, con respecto a las variables consideradas. Sin embargo, esta hipótesis es muy poco verosímil ya que la presencia de accidentes orográficos, del mar o de lagos o de barreras artificiales impide el crecimiento de las áreas metropolitanas en ciertas direcciones; e, igualmente, la existencia de grandes vías de comunicación, de otras entidades de población cercanas o de ciertas tendencias tradicionalmente establecidas pueden facilitar, en cambio, el crecimiento en mayor medida hacia algunas otras direcciones.

        Con todo, y en la medida en que, en términos generales, puede aceptarse la "difusión con la distancia al lugar central", se puede modelizar una situación más general y más realista considerando, simplemente, que la variación de las características metropolitanas en el espacio social se debe a dos efectos independientes: la difusión con la distancia y la concentración/difusión con la distancia angular a algunas direcciones de especial consideración.

    De esta forma cada característica estudiada puede considerarse como función de la distancia y de la dirección , (lo que supone expresar su variación en coordenadas polares), de forma que puedan expresarse ambos efectos independientemente:   

 siendo r , el radio del vector de posición (distancia al centro) y siendo , la dirección.

    Escoger un modelo multiplicativo es justificable, basándonos en que el efecto (medio) debido a la distancia, se ve afectado por un factor corrector aumentativo o diminutivo debido a la dirección (relativa a algunas direcciones potenciadoras o atenuadoras).

    Considerando la variación con la distancia, R(r), la ya establecida en el modelo simplificado, el problema se centra en establecer una adecuada función para el factor corrector direccional.
     Este factor, Z() , debe ser tal que amplifique (o reduzca) el efecto de R(r) en las direcciones próximas a cada dirección potenciadora (o atenuadora) ,que para simplificar podemos llamar polo (negativo o positivo).

    Si suponemos la existencia de n polos, la función Z() deberá cumplir las siguientes características:

• Presentar un extremo local en cada ,siendo un máximo y tomando un valor superior a 1,si es un polo positivo (potenciador); y siendo un mínimo y tomando un valor inferior a 1 si se trata de un polo negativo.

• Ser simétrica respecto a cada polo en un cierto entorno del mismo

• Decrecer con la distancia angular a cada polo si éste es positivo o crecer con la distancia angular si el polo es negativo.

• En cierto entorno de cada polo la influencia de la distancia angular a los demás polos debe ser despreciable

• Y, además debe ser positiva

    Es conveniente, también, que pueda ser descompuesta en el producto de n funciones que recojan separadamente el efecto de la difusión alrededor de cada polo:         

    Una función que cumple las propiedades anteriores y que presenta notables ventajas de cara a la modelización y a la eventual estimación es la función:    

    En donde es un paramétro positivo para los polos positivos y negativo para los negativos que coincide con el logaritmo del factor máximo ( o mínimo) de corrección por la cercanía a un polo; es pues un parámetro de intensidad polar. Y donde k_j es un parámetro de concentración del efecto polar alrededor del polo, que debe ser lo suficientemente grande para permitir que los efectos de los polos distantes sean despreciables.

De esta forma la función Z() quedaría como:   

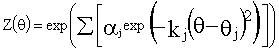
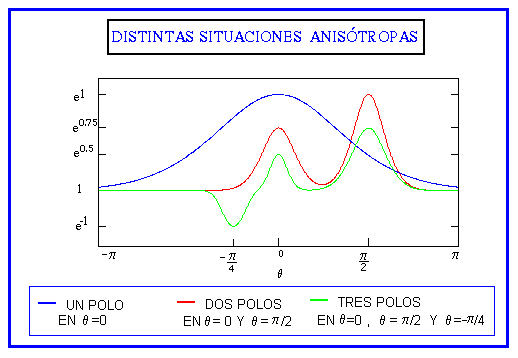
    En el siguiente gráfico se muestran distintas situaciones anisótropas, representadas por funciones de este tipo:(Los máximos y mínimos en las direcciones polares se corresponden con los valores de , en cada polo  ).

    De esta forma el modelo general para la variación de una característica metropolitana quedaría como:

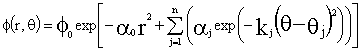
    Hay que hacer notar, que los parámetros no podrían ser estimados por regresión aunque tomáramos logaritmos, por lo que en aras de la versatilidad práctica del modelo deberían ser establecidos a priori, según algún criterio.

    En este sentido, un criterio apriorístico plausible es considerar que la concentración alrededor de cada polo debe ser tal que los efectos de la distancia a los otros polos fueran despreciables. Así, por ejemplo, considerar que el efecto de los otros polos debe ser del orden de 10^-5 nos llevaría a considerar que cada toma el valor:

    Haciendo esta consideración no sería necesaria la estimación de estos parámetros y el modelo podría estimarse por regresión tomando logaritmos, ya que:

resultando un modelo lineal entre las variables       

    Obviamente las isopletas, en este caso general, ya no serían circulares sino que presentarían irregularidades direccionales.Las isopletas ,k(r,q,C), expresadas en coordenadas polares, correspondientes a cada valor constante de , , vendrían dadas por la expresión:

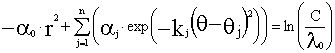
Llamando a cada expresión: nos quedaría:

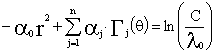
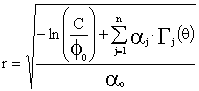
Y para obtener la ecuación de la isopleta =C en coordenadas cartesianas, bastaría considerar x=r.cos(θ) e y=r. sen(θ)

En el siguiente gráfico se muestran distintas isopletas en una situación en la que existen dos polos positivos en las direcciones 0 y π/4. La intensidad de ambos polos es la misma con α₁=α₂= 0.075 y el efecto de la distancia viene expresado con un valor del parámetro α₀= 0.5

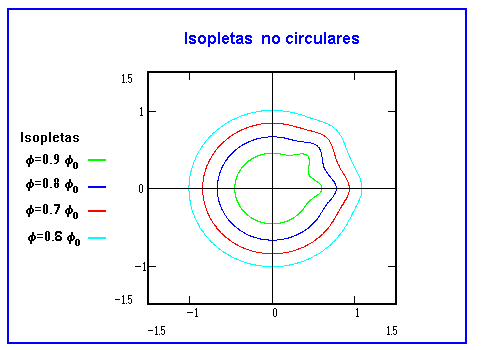
    Puede argumentarse que la isopleta-pared, que nos delimitará el Área Metropolitana será la correspondiente a Con lo que las coordenadas polares de la pared metropolitana en cada polo serán:
                                                                  .

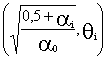
    En otro orden de cosas, establecidos a priori los parámetros de concentración polar, el modelo sería fácil de estimar por regresión, e igualmente podríamos generalizarlo para el caso de considerar varias características metropolitanas,, sin más que estimar el modelo sobre la variable indicador-general : , con:

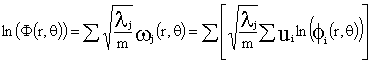
donde es la j-ésima componente principal: ,siendo las u_j las correspondientes ponderaciones factoriales y donde las son los correspondientes valores propios de cada componente principal.

?