3. EL MODELO ANISÓTROPO DE DIFUSIÓN CON LA DISTANCIA.

3.2.Determinación del Área Metropolitana

La pared que nos delimitaría el Área Metropolitana vendría dada por el conjunto de puntos ( la curva ) en la que se hiciera máximo el módulo del gradiente de f ,esto es,en el que se maximice ||grad ||

    Teniendo en cuenta que nos viene expresada en coordenadas polares, el procedimiento de determinación de la pared puede resultar bastante complejo .Existe, sin embargo, un procedimiento aproximado mucho más simple que nos conduce a una aceptable solución del problema:

    Este procedimiento consiste en fijar una dirección y encontrar un punto de la pared, para posteriormente considerar que la pared es " aproximadamente" la isopleta que contiene al punto encontrado. Teniendo en cuneta que no presenta simetría circular, la pared no coincidirá exactamente con ninguna isopleta, pero si consideramos que sólo se aleja significativamente de la simetría circular en las direcciones cercanas a los polos y si el número de éstos no es excesivo, en general, la pared acabará coincidiendo con una cierta isopleta en casi todos sus puntos, presentando las máximas discrepancias en las direcciones polares. Con todo estas discrepancias son aproximadamente iguales al cociente ln(r*)/r*, siendo r* el valor de la distancia a la pared en cada dirección polar considerada. Esto supone, en la práctica, unos errores máximos del orden de unas decenas de metros, lo que queda de sobra compensado por el ahorro de cálculo.
    Así pues, y siguiendo este método aproximado, si consideramos, sin pérdida de generalidad, que la dirección del eje de las X no es una de las direcciones polares, es relativamente simple ver que en esta dirección el punto de máximo módulo del gradiente es el que corresponde a una distancia r que verifica que:

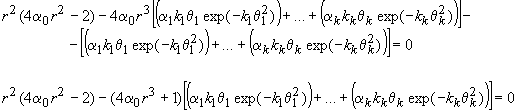
Si tenemos en cuenta que es un factor del orden de 10^-5, puede considerase que la pared en la dirección está situada aproximadamente a una distancia , cometiendo, en la práctica, un error de algunos decímetros.

    En consecuencia, puede argumentarse que la pared, que nos delimitará el Área Metropolitana se aproxima mucho a la isopleta : , Obteniéndose un criterio de delimitación similar al caso isótropo.

    Como se ha comentado ya, establecidos a priori los parámetros de concentración polar, el modelo sería fácil de estimar por regresión. También podría generalizarse para el caso de considerar varias características metropolitanas,, sin más que estimar el modelo sobre la variable indicador-general : , análogamente al caso isótropo.