GUÍA DIDÁCTICA
Rafael Pla López
Departament de Matemàtica Aplicada
Universitat de València
2010
Objetivos:
Específicos:
- Estimar los distintos tipos de error que se producen en la resolución de problemas por métodos numéricos.
- Obtener aproximaciones sucesivas a la solución de un sistema de ecuaciones lineales Ax=b.
- Resolver por aproximaciones sucesivas una ecuación no lineal del tipo f(x)=0.
- Encontrar una función polinómica que pase por un conjunto de puntos.
- Obtener una solución aproximada
de la
integral definida de
una función, ∫ab
f(x)dx .
- Aprender a trabajar en equipo.
- Aprender a exponer públicamente un trabajo.
- Adquirir respeto por l@s compañer@s que exponen un trabajo, atendiéndoles y ayudàndoles en caso necesario.
- Aprender a realizar razonamientos deductivos para demostrar un enunciado a partir de determinadas premisas.
- Adquirir la capacidad de cuestionar la fiabilidad de los resultados obtenidos por métodos numéricos.
Metodología:
- Trabajo en clase en grupos pequeños, debatiendo textos, demostrando enunciados y resolviendo problemas, seguido de su exposición pública.
- Trabajo en equipo fuera de clase, elaborando trabajos para su presentación al profesor.
- Trabajo pràctico en aula de informàtica, confeccionando programas para la resolución de problemas, ejecutàndolos para obtener sus resultados, y valorando dichos resultados, reflejando todo ello en una memoria de cada pràctica.
- Aubanell, A., Benseny, A., Delshams, A. (1991), Eines bàsiques de Càlcul Numèric, Universitat Autònoma de Barcelona, Bellaterra
- Aubanell, A., Benseny, A., Delshams, A. (1993), Útiles bàsicos de Càlculo Numérico, Editorial Labor, Barcelona
- Conte, S.D., de Boor, C. (1985), Anàlisis Numérico, McGraw-Hill, México
- Martínez Salas, J. (1989), Métodos Matemàticos, Ed.el autor, Valladolid
- Aràndiga, F. (2002), Càlcul Numèric, Departament de Matemàtica Aplicada, Universitat de València
- La calificación final serà la media de la nota de teoría y la nota de pràcticas, siempre que ambas sean igual o superior a 4 (sobre un màximo de 10).
- Para la nota de teoría puntuarà hasta 8 puntos la evaluación de un examen final individual escrito, y hasta 2 puntos la realización de trabajos en equipo, que solamente podràn considerarse en caso de asistencia regular a clase (en caso contrario, deberàn responderse cuestiones adicionales en el examen final puntuables hasta los 2 puntos restantes). Se podrá utilizar un formulario escrito a mano personalmente en un máximo de 5 hojas sin problemas resueltos (no se admiten fotocopias). Ademàs, se primarà la participación activa en clase sumando una décima por cada exposición pública de un trabajo realizado en clase.
- Para la nota de pràcticas, sobre la base de la asistencia
obligatoria a las mismas, se valorarà la memoria presentada de
cada pràctica, que deberà contener los programas
elaborados, los resultados obtenidos con ellos y la valoración
de los mismos.
Tema
0: Estimar
los distintos tipos de error que se
producen en la
resolución de problemas por métodos numéricos:
Objetivos:
- Comprender la diferencia entre errores intrínsecos e instrumentales.
- Comprender los conceptos de error absoluto y error relativo.
- Entender cómo tratan los ordenadores los números no enteros.
- Estimar cuántas cifras significativas se conocen de una determinada cantidad.
- Debatir un texto en grupos pequeños, poniendo posteriormente en común el resultado del debate.
- Realización de tareas en grupos pequeños, exponiendo públicamente a continuación sus conclusiones.
Actividad 1. Debatir en grupos pequeños el siguiente texto, escogiendo previamente un portavoz de cada grupo para exponer posteriormente las conclusiones y en su caso las dudas suscitadas:
Los métodos numéricos permiten obtener soluciones aproximadas a determinados problemas. Por evaluar estas soluciones, es importante tener una estimación del error.
Hay errores intrínsecos al método utilizado. Normalmente estos errores se pueden hacer tan pequeños como se quiera, a través de aproximaciones sucesivas. Aun así, al disponer de un tiempo finito por realizar los cálculos, debemos conformarse con aproximar con un cierto margen de error. Hará falta, pues, un compromiso entre la cota de error admitida y el tiempo máximo de cálculo que nos podemos permitir.
Naturalmente, serán preferibles aquellos métodos que permetan aproximar hasta una determinada cota de error en menos tiempo, los cuales diremos que tienen una velocidad de convergencia mayor. En los métodos que aproximan iterativamente a través de una serie de pasos sucesivos, podemos mesurar esta velocidad por la inversa del número de pasos necesarios. Aun así, desde el punto de vista del tiempo de cálculo hace falta valorar también la complejidad de los cálculos a realizar en cada paso.
A los efectos anteriores, normalmente trabajaremos con elerror absoluto, definido como el valor absoluto de la diferencia entre el valor exacto x y la aproximación
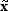 ,
, Definición 1: ε = | x -
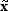 |
| Naturalmente, al desconocer el valor exacto el único que podremos hacer es estimar el error, dando una cota superior para el mismo.
Hay también errores instrumentales debidos al instrumento de cálculo utilizado. En particular, las calculadoras y ordenadores digitales trabajan con un número finito de cifras y por lo tanto no utilizan números con infinitas cifras decimales, como los irracionales o los fraccionarios "decimales periódicos". Por ejemplo, aproximarían 1/3 = 0' 3 ≈ 0'333333 , con un número de cifras decimales dependiente de la precisión del instrumento.
Por aproximar el cálculo de los números racionales y reales, los ordenadores trabajan con números decimales en punto flotante, tratando por separado las cifras significativas (mantisa) y el orden de magnitud (característica). Por ejemplo, 0'0000000000000235410347= 2'35410347.10-14 se expresará como 2.35410347E-14.
Comoquiera que la principal limitación está en el número de cifras significativas admitidas, lo que nos importará será el error relativo del valor aproximado
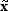 respecto del valor exacto x, definido cómo
respecto del valor exacto x, definido cómoDefinición 2: εr = | x -
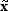 | / | x |
| / | x |Actividad 2. Obtener
una
fórmula que conociendo el error relativo y la mantisa nos
proporcione el número de cifras significativas exactas que
conocemos, de acuerdo con la
Definición 3:
Diremos que 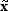 =aEb
(con 1≤
a<10) aproxima a x
con un
número entero de k
cifras significativas si y sólo si
=aEb
(con 1≤
a<10) aproxima a x
con un
número entero de k
cifras significativas si y sólo si
La obtención de dicha fórmula nos permitirá completar el enunciado del siguiente
Teorema 1:
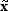 =aEb
aproximará a x
con un
número de cifras
significativas exactas k
igual
al mayor número entero menor que
=aEb
aproximará a x
con un
número de cifras
significativas exactas k
igual
al mayor número entero menor que ¿Como podríamos interpretar el caso en que k resultara negativo?
Actividad 3.
Problema 1: calcular el error absoluto y relativo en los siguientes casos:
a)
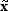 = 2.35410347E-14, x = 2.35410343E-14
= 2.35410347E-14, x = 2.35410343E-14b)
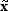 = 2.35410347E16, x = 2.35410343E16
= 2.35410347E16, x = 2.35410343E16¿Con cuántas cifras significativas aproxima
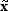 a x?
a x?Trabajo 1 (para su realización en equipo):
a) Ampliar la clasificación de los errores planteada en la Actividad 1 a partir de la bibliografía recomendada.
b) Poner distintos ejemplos de aproximación de
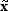 a x con
distintos errores absolutos y
relativos y calcular el número de cifras significativas con que
se aproxima en cada caso. Evaluar de qué depende dicho
número. Considerar algún caso en que el error relativo
sea mayor a 0'5 y valorarlo.
a x con
distintos errores absolutos y
relativos y calcular el número de cifras significativas con que
se aproxima en cada caso. Evaluar de qué depende dicho
número. Considerar algún caso en que el error relativo
sea mayor a 0'5 y valorarlo.Tema 1: Obtener aproximaciones sucesivas a la solución de un sistema de ecuaciones lineales Ax=b :
Objetivos:
- Encontrar criterios de convergencia para una transformación x(k+1) = G(x(k)) tal que A(lim k→∞ x(k)) = b
- Encontrar una condición suficiente para la existencia de una solución única de una ecuación de iteración lineal de punto fijo x=Bx+c
- Encontrar criterios de convergencia para una iteración lineal de punto fijo x=Bx+c
- Transformar un sistema de ecuaciones lineales Ax=b en una iteración lineal de punto fijo x=Bx+c equivalente
- Encontrar una condición suficiente para que dicha transformación genere una iteración lineal de punto fijo convergente
- Aproximar iterativamente la solución de un sistema de ecuaciones lineales Ax=b utilizando como aproximación a la matriz A su matriz diagonal D (método de Jacobi)
- Obtener la iteración lineal de punto fijo equivalente al sistema Ax=b por el método de Jacobi.
- Encontrar una condición para la matriz A que garantice que dicha iteración lineal de punto fijo sea convergente.
- Evaluar un sistema de ecuaciones lineales y adaptarlo en su caso para que cumpla la condición de convergencia
- Aproximar iterativamente la solución de un sistema de ecuaciones lineales Ax=b utilizando como aproximación a la matriz A su matriz triangular inferior L+D (método de Gauss-Seidel)
- Encontrar una expresión simplificada en función de L, D y U de la matriz B de la iteración lineal de punto fijo x=Bx+c, equivalente al sistema Ax=b con A=L+D+U, obtenida por el método de Gauss-Seidel.
- Encontrar una expresión que nos permita calcular sucesivamente los diferentes componentes del vector x(k+1) .
- Discutir la convergencia de la iteración lineal de punto fijo obtenida por el método de Gauss-Seidel
- Deducir enunciados lógicamente, trabajando en la medida de lo posible en grupos pequeños para exponer públicamente a continuación su demostración.
- Resolver problemas en grupos pequeños y exponer públicamente a continuación su resolución.
- Trabajar en aula de informática elaborando programas para la resolución iterativa de sistemas de ecuaciones lineales, ejecutándolos para la resolución de un sistema determinado y evaluando su velocidad de convergencia.
Actividad 1. Definiendo la norma matricial asociada a una norma vectorial por
Definición 4: ||A|| = max x≠0 ||Ax||/||x||
con lo que se cumple
Teorema 2: ||Bx|| ≤ ||B||·||x||
demostrar por reducción al absurdo que
Teorema 3: Si ||B||<1 & x=Bx , entonces x=0
Actividad 2. Recordando cuál es la condición necesaria y suficiente para que:
a) un sistema homogéneo de ecuaciones lineales como x=Bx tenga solución única x=0
b) un sistema inhomogéneo de ecuaciones lineales como x=Bx+c tenga solución única,
demostrar que
Teorema 4: Si ||B||<1, entonces x=Bx+c tiene solución única
Actividad 3. Recordando que, por las propiedades de los números naturales, habremos demostrado por inducción matemática que una propiedad se cumple para todo número natural k si se cumple para k=0 y podemos demostrar que, suponiendo que se cumple para k, se cumplirá para k+1, [p0 & (k) (pk→ pk+1)]→ (k) pk , demostrar que
Teorema 5: Si x=Bx+c & para todo número natural k, x(k+1)=Bx(k)+c, entonces para todo número natural k, x-x(k)=Bk(x-x(0)) .
Actividad 4. Recordando que podemos deducir que una sucesión no negativa tenderá a cero si está acotada superiormente por otra sucesión que tiende a cero, demostrar que
Teorema 6: Si ||B||<1 & para todo número natural k, x(k+1)=Bx(k)+c, entonces existe x tal que x=Bx+c & x=lim k→∞ x(k) .
Actividad 5. Recordando que, si x=Bx+c & x(k)=Bx(k-1)+c, entonces x-x(k)=B(x-x(k-1)), así como la propiedad triangular
Teorema -1: ||x-x(k-1)|| ≤ ||x-x(k)|| + ||x(k)-x(k-1)||
demostrar que
Teorema 7: Si x=Bx+c & x(k)=Bx(k-1)+c & ||B||<1, entonces podemos acotar el error de aproximación de x(k) a x por
||x-x(k)|| ≤ ||x(k)-x(k-1)||·||B||/(1-||B||) .
Actividad 6. Demostrar que, siendo I=(δij)i,j=1...n la matriz identidad (cuyos elementos valen 1 si i=j y 0 si i≠j) y A, B, C matrices n por n, se cumple que
Teorema 8: Si B=I-C-1A & c=C-1b, entonces x=Bx+c es equivalente a Ax=b .
Actividad 7. Demostrar que, definiendo
Definición 5: C es una buena aproximación a A, C≈A, si y sólo si ||I-C-1A||<1
se cumple que
Teorema 9: Si C≈A & B=I-C-1A & c=C-1b & para todo número natural k, x(k+1)=Bx(k)+c, entonces A(lim k→∞ x(k))=b .
Actividad 8. Recordando que la inversa de la matriz diagonal D=((δijAii)i,j=1...n es
Teorema -2: D-1=((δij/Aii)i,j=1...n
que los productos matriciales se calculan mediante (XY)ij=∑ k XikYkj y que ∑ k δikXk = Xi, demostrar que
Teorema 10: Si C=D & B=I-C-1A & c=C-1b , entonces, para todo i,j=1...n, ci=bi/Aii & Bij = -Aij/Aii si i≠j & Bij=0 si i=j .
Actividad 9. Obtener la expresión de la iteración correspondiente al método de Jacobi,
Teorema 11: x(k+1)i =
Actividad 10. A partir de las siguientes definiciones:
Definición 6: Diremos que la matriz A es estrictamente diagonalmente dominante por filas si y sólo si, para todo i=1...n,
|Aii| > ∑ j≠i |Aij|
Definición 7: ||x||∞ = max i |xi|
y sabiendo que
Teorema -3: ||A||∞ = max i ∑ j=1n |Aij|
demostrar que
Teorema 11: Si la matriz A es estrictamente diagonalmente dominante por filas, entonces la iteración correspondiente al método de Jacobi es convergente.
Actividad 11.
Problema 2: Aproximar la solución del sistema de ecuaciones
{10x1+x2+x3=12, x1+10x2+x3=12, x1+x2+10x3=12} por el método de Jacobi: iterar desde (x1,x2,x3)=(0,0,0) hasta que ||x(k)-x(k-1)||∞<0.005 ; acotar el error.
¿Qué pasaría si tomáramos el sistema de ecuaciones
{x1+10x2+x3=12, x1+x2+10x3=12, 10x1+x2+x3=12}?
Actividad 12. Siendo Lij=Aij si i>j, Lij=0 si i≤j, Uij=Aij si i<j, Uij=0 si i≥j, de modo que

Teorema 12: Si C=L+D & B=I-C-1A, entonces B=
Actividad 13. Recordando que c=C-1b, obtener la expresión matricial de la iteración correspondiente al método de Gauss-Seidel,
Teorema 13: x(k+1) =
Actividad 14. Aplicar D-1(L+D) a ambos términos de la expresión anterior y reescribir la expresión resultante en la forma
Teorema 14: x(k+1) = D-1( )
Actividad 15. Obtener una expresión que nos permita calcular sucesivamente los distintos componentes
Teorema 15: x(k+1)i =
Desarrollar dicha expresión para el caso n=3
Actividad 16. Discutir las condiciones de convergencia del método de Gauss-Seidel.
Actividad 17.
Problema 3: Aproximar la solución del sistema de ecuaciones
{10x1+x2+x3=12, x1+10x2+x3=12, x1+x2+10x3=12} por el método de Gauss-Seidel: iterar desde (x1,x2,x3)=(0,0,0) hasta que ||x(k)-x(k-1)||∞<0.005 ; comparar su velocidad de convergencia con el método de Jacobi.
Trabajo 2 (para su realización en equipo):
Aproximar la solución del sistema de ecuaciones {5x+y=6, x+4y=5} por el método de Jacobi a partir de x(0)=(2,2) y de x(0)=(10,0) hasta que se cumpla ||x(k)-x(k-1)||∞<0.05 , representando gráficamente en el plano los sucesivos puntos encontrados.
Aproximar dicha solución por el método de Gauss-Seidel a partir de x(0)=(2,2), representando gràficamente en el plano los sucesivos puntos encontrados.
Aplicar el método de Jacobi a partir de x(0)=(2,2) con el sistema escrito de esta forma: {x+4y=5, 5x+y=6}, representando gràficamente en el plano los sucesivos puntos encontrados.
Comparar las distintas iteraciones, valorando su convergencia.
Tema 2: Resolver por aproximaciones sucesivas una ecuación no lineal del tipo f(x)=0 :
Objetivos:
- Desarrollar un algoritmo que nos permita ir acotando en intervalos cada vez más pequeños una solución de la ecuación f(x)=0 teniendo en cuenta el signo de f(x) en los extremos de un intervalo.
- Desarrollar un algoritmo que nos permita ir aproximándonos cada vez más a una solución de la ecuación f(x)=0 teniendo en cuenta el valor de f(x) en los extremos de un intervalo.
- Desarrollar un algoritmo que nos permita ir acotando en intervalos tan pequeños como queramos una solución de la ecuación f(x)=0 teniendo en cuenta el valor de f(x) en los extremos de intervalos sucesivos.
- Desarrollar un algoritmo que nos permita ir aproximándonos cada vez más a una solución de la ecuación f(x)=0 teniendo en cuenta el valor de f(x) en un punto y su derivada.
- Entender las dificultades
que se encuentran con los distintos algoritmos para aproximarse o
acotar una solución de la ecuación f(x)=0.
- Estudiar la velocidad de convergencia de una sucesión que tienda a una solución de la ecuación f(x)=0.
- Desarrollar un algoritmo que permita converger lo más ràpidamente posible hacia una solución de la ecuación f(x)=0.
- Reflexionar colectivamente, en grupos pequeños y en el conjunto de la clase, sobre distintos procedimientos para aproximarse a una solución de la ecuación f(x)=0.
- Deducir el orden de convergencia de distintos métodos de búsqueda de una solución de la ecuación f(x)=0, en clase (en grupos pequeños exponiendo a continuación las conclusiones obtenidas) y a través un trabajo en equipo.
- Trabajar en aula de informática elaborando programas para aproximar una solución de la ecuación f(x)=0, ejecutarlos y valorar los resultados obtenidos.
Actividad 1: teniendo en cuenta el Teorema de Bolzano,
Teorema -4: Para todo intervalo [a,b] de números reales, y toda función continua f : [a,b]→R, si f(a)·f(b)<0, entonces existe un número xc[a,b] tal que f(x)=0,
si se cumple la premisa del teorema y tomando inicialmente u=a & v=b, calculando w=(u+v)/2 y examinando el signo de f(w), estudiar qué nuevo intervalo deberíamos tomar para seguir acotando la solución (método de la Bisección).
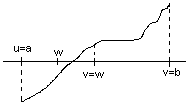
Puede encontrarse un modelo de algoritmo en http://www.uv.es/~pla/Tutoria/mniq/algorit1.gif
Si reiteramos el proceso hasta que la longitud del intervalo sea menor que una tolerancia ε, ¿de qué dependerá, en general, el número de veces que debamos reiterarlo?
Actividad 2.
Problema 4: Si a=0, b=8, ε=0.25, ¿cuántos pasos serán necesarios como máximo para llegar a una solución aproximada con esa cota de error? Obtener una expresión general que nos dé el número de pasos en función de a, b y ε.
Actividad 3.
Suponiendo a<b
& f(a)·f(b)<0 y tomando inicialmente u=a & v=b,
obtener la ecuación de la recta que pasa por los puntos (u,f(u))
& (v,f(v)) y calcular el punto (w,0) en que corta al eje de
abcisas,
w = |
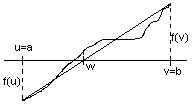 |
Puede experimentarse gràficamente con un "applet" en http://www.apropos-logic.com/nc/RegulaFalsiAlgorithm.html
Puede encontrarse un modelo de algoritmo en http://www.uv.es/pla/Tutoria/mniq/algorit2.gif
Actividad 4.
Problema 5: Aplicar el método de Regula-Falsi en la figura adjunta hasta que la longitud del intervalo sea menor a la del segmento indicado (ε):
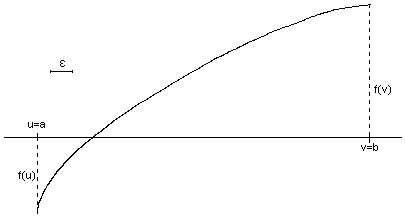
Actividad 5.
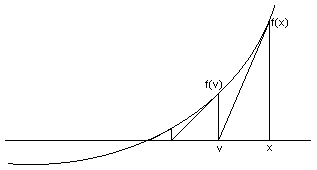
Problema 6. Repetir el problema anterior en la figura adjunta modificando el método seguido de modo que cuando dos valores intermedios w consecutivos nos den valores de f(w) con el mismo signo, en vez de volver a trazar la recta hasta el mismo punto que en el paso anterior, se trace hasta un punto con la mitad de la ordenada, según se muestra en la figura pequeña (método de Regula-Falsi modificado)


Puede experimentarse gráficamente con un "applet" (adaptado para Netscape 4.5) en http://www.uv.es/pla/java/Regulafa.html
Actividad 6. Calculando para un valor x los valores de la función f(x) y de su derivada f '(x), obtener la ecuación de la recta tangente correspondiente (recta que pasa por el punto (x,f(x)) de pendiente f '(x) ) y calcular el punto (v,0) en que corta al eje de abcisas,
v = |
 |
Puede encontrarse un modelo de algoritmo en http://www.uv.es/pla/Tutoria/mniq/algorit4.gif
Puede experimentarse gráficamente con un "applet" (adaptado para Netscape 4.5) en http://www.uv.es/pla/java/Newton.html
Actividad 7.
Problema 7: Aplicar el método de Newton a la ecuación f(x)=2x/(1+x2) a partir del punto x=1/3½ (hacer los cálculos sin aproximar). Interpretar el resultado a partir de la figura adjunta.
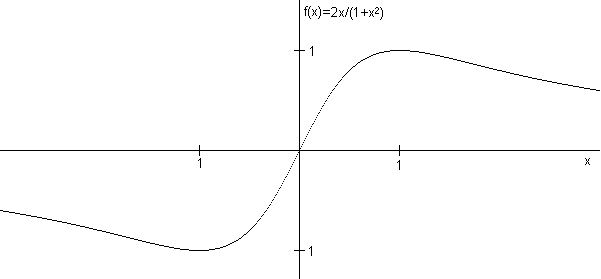
Actividad 8.
Definiendo el orden de
convergencia
de una sucesión por la
Definición 8:
Dados pcR+,
αcR
y la
sucesión de números reales (xn)ncN
tal que
α=lim n→∞ xn,
diremos que dicha sucesión tiene orden de convergencia p si y
sólo si existe un número real L≠0 tal que
& si p=1, entonces |L|<1
Teorema -5: Para todo intervalo [a,b] de números reales, toda función real continua y derivable hasta segundo orden en dicho intervalo, fcC2([a,b],R), y todo par de números α,xc[a,b], existe ξc[α,x] tal que
Teorema 16: Para todo fcC2([x0,y0],R), x0,y0cR tales que f(x0)·f(y0)≠0, si para todo ncN,
xn+1 = xn - f(xn)(yn-xn)/(f(yn)-f(xn))
yn+1 = yn
& α = lim n→∞ xn
& para todo xc[x0,y0], f "(x)≠0,
entonces existe ηc[α,y0] tal que
Actividad 9.
Problema 8: Examinar la figura adjunta para determinar cuál es, en las condiciones del Teorema 16, el signo de
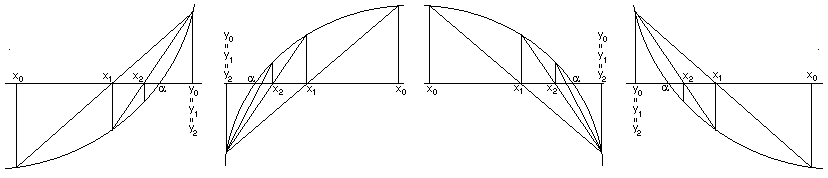
Actividad 10. Demostrar el
Teorema 17: Para toda fcC2([x0,y0],R) con x0,y0cR tales que f(x0)·f(y0)≠0 & para todo xc[x0,y0], f "(x)≠0 , el método de Regula-Falsi tiene orden de convergencia 1.
Actividad 11. Aplicando el desarrollo en serie de Taylor de f(x) hasta el segundo orden, así como el desarrollo en primer orden de f '(x),
Teorema -6: Para todo intervalo [a,b] de números reales, toda función real continua y derivable hasta segundo orden en dicho intervalo, fcC2([a,b],R), y todo par de números α,xc[a,b], existe ξc[α,x] tal que
Teorema 17: Para todo subconjunto A de R y toda fcC2(A,R), α,x0cA, si para todo ncN,
xn+1 = xn - f(xn)/f '(xn) c A
& α = lim n→∞ xn
& f(α)=0 & f '(α)≠0 (raíz simple)
& f "(α)≠0
entonces el método de Newton tiene orden de convergencia 2.
¿Qué podría pasar si f "(α)=0?
Actividad 12.
Demostrar el
Teorema 18:
Para todo
subconjunto A de R y toda fcC2(A,R),
α,x0cA, si
para todo ncN,
xn+1 =
xn
- f(xn)/f '(xn)
c
A
& α = lim n→∞ xn
& f(α)=0 & f '(α)=0 (raíz
múltiple)
entonces el método de Newton tiene orden de convergencia 1.
Actividad 13.
Utilizando la
expresión del desarrollo en serie de Taylor hasta el orden m+1,
Teorema -7:
Para todo
intervalo [a,b] de números reales, toda función real
continua y derivable hasta orden m+1 en dicho intervalo, fcCm+1([a,b],R),
y todo par de números α,xc[a,b],
existe ξc[α,x]
tal que
Teorema -8: Para todo mcN, (m+1)! = (m+1) m!
demostrar el
Teorema 19: Para todo subconjunto A de R y toda fcCm+1(A,R), α,x0cA, si para todo ncN,
xn+1 = xn - m·f(xn)/f '(xn) c A (método de Newton modificado)
& α = lim n→∞ xn
& para todo i=0,1,...m-1, f (i)(α)=0 & f (m)(α)≠0 (raíz de multiplicidad m)
& f (m+1)(α)≠0
entonces la sucesión (xn)ncN tiene orden de convergencia 2.
¿Qué podría pasar si f (m+1)(α)=0?
| Actividad
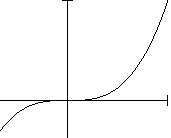
14. Problema 9: Aplicar el método de Newton (modificado en su caso) a la ecuación f(x) = x3 = 0, representada en la figura adjunta. ¿Cuál podría ser su orden de convergencia? |
 |
Trabajo 3 (para su realización en equipo):
Obtener algebraicamente las soluciones de la ecuación x2-5x+6=0 .
Aplicar el método de Newton para aproximarse a una solución α a partir del valor inicial x0=1 hasta llegar a una distancia menor a 0'1 de dicha solución.
Calcular
limxn→α (xn+1-α)/(xn-α)2 para comprobar que la sucesión generada por el método de Newton a partir de x0=1 tiene orden de convergencia 2 .
Tema 3: Encontrar una función polinómica que pase por un conjunto de puntos:
Objetivos:
- Demostrar la existencia y unicidad del polinomio interpolador de grado menor o igual que m que pasa por m+1 puntos de abcisas distintas.
- Encontrar una fórmula que nos dé directamente la expresión del polinomio interpolador.
- Encontrar un método para obtener sucesivamente puntos interpolados a medida que introducimos nuevos puntos para interpolar.
- Encontrar un método que nos dé sucesivos
términos del polinomio interpolador.
- Encontrar un método para interpolar conociendo las ordenadas de un conjunto de puntos y algunas derivadas en los mismos.
- Entender los problemas de fiabilidad
de la interpolación, especialmente si se realiza fuera del
intervalo en el que se tienen datos (extrapolación) o se
utilizan polinomios de un grado elevado.
- Deducir enunciados lógicamente, trabajando en la medida de lo posible en grupos pequeños para exponer a continuación públicamente su demostración.
- Aplicar algoritmos para resolver problemas en grupos pequeños, exponiendo a continuación públicamente su resolución.
- Trabajar en aula de informática elaborando programas para interpolación y regresión lineal, ejecutarlos y valorar los resultados obtenidos.
Actividad 1. Teniendo en cuenta la condición necesaria y suficiente para que un sistema de ecuaciones lineales sea determinado, el valor del determinante de Vandermonde
Teorema -9: |xki| = ∏ k>i (xk-xi)
y la
Definición 9: Diremos que p(x) = ∑ i=0 m ai xi es un polinomio interpolador de grado menor o igual que m en los puntos {(xk,fk) / k=0,1...m} si y sólo si, para todo k=0,1...m, p(xk)=fk ,
demostrar el
Teorema 20: Si para todo i≠k, xi≠xk, entonces existe un único polinomio interpolador de grado menor o igual que m en los puntos {(xk,fk) / k=0,1...m} .
Actividad 2. Teniendo en cuenta que
∑ i=0 m Ξi = Ξk + ∑ i≠k Ξi para todo k=0,1...m, y que
∏ j≠i Ξkj = Ξkk·∏ j≠i & j≠k Ξkj para todo i≠k
demostrar el
| Teorema 21: Si para todo i≠k, xi≠xk, entonces p(x) = ∑ i=0 m fi | ∏
j≠i (x-xj) ∏ j≠i (xi-xj) |
Actividad 3.
Problema 10: Dados los puntos
| x
k |
1 |
2 |
4 |
5 |
| f
k |
0 |
2 |
12 |
21 |
(sugerencia: al aplicar la fórmula, escribir primero cada denominador para evitar errores)
Actividad 4. Demostrar el
Teorema 22: Si para todo i,j=0,1...m, si i≠k, entonces xi≠xk,
& si i+j≤m , entonces pi,j es el polinomio interpolador de grado menor o igual que j en {(xk,fk) / k=i,i+1...i+j},
entonces para todo j=1...m, i=0,1...m-j,
| pi,j(x)
= |
(xi+j-x)pi,j-1(x)
+ (x-xi)pi+1,j-1(x) xi+j - xi |
Actividad 5. Teniendo en cuenta que, con los pi,j definidos en el Teorema 22,
Teorema 23: para todo i=0,1...m & para todo xcR, pi,0(x) = f i
y
Teorema 24: p0,m es el polinomio interpolador de grado menor o igual que m en {(xk,fk) / k=0,1...m} ,
utililizar el algoritmo
 (método
de Neville)
(método
de Neville)para resolver el
Problema 11: Dados los puntos
| x
k |
1 |
2 |
4 |
| f
k |
0 |
2 |
12 |
Añadir a continuación el punto (x3, f3) = (5, 21) y obtener la nueva interpolación para x=3 .
Comparar el resultado obtenido con el del problema 10.
Actividad 6. De acuerdo con la
Definición 10: Con {(xk,fk) / k=0,1...m} tal que para todo i,j=0,1...m, si i≠k, entonces xi≠xk, definiremos las diferencias divididas f[xi,xi+1,...xj] mediante
| f[xi]
= |
fi | para
todo i=0,1...m |
| f[xi,xi+1,xj]
= |
f[xi+1,...xj]
- f[xi,...xj-1] xj - xi |
para
todo i=0,1...m-1,
j=i+1,...m |
| f[x0] f[x1] f[x2] f[x3] |
> f[x0,x1] > f[x1,x2] > f[x2,x3] |
>
f[x0,x1,x2] > f[x1,x2,x3] |
>
f[x0,x1,x2,x3] |
| k |
0 |
1 |
2 |
3 |
| x
k |
1 |
2 |
4 |
5 |
| f
k |
0 |
2 |
12 |
21 |
Actividad 7. Recordando que, de acuerdo con la fórmula de Taylor
Teorema -10: pm(x) = ∑j=0 m [ f (j)(x0) / j! ] (x-x0)j es el polinomio de grado menor o igual que m que cumple las condiciones pm(j)(x0)=f(j)(x0) para j=0,1...m
así como que
Teorema -11: limx→xi (f(x)-f(xi))/(x-xi) = f '(xi)
tomaremos
Definición 11: f[xi,xi+1,...xj] = f (j-i)(xi)/(j-i)! si xi=xi+1=...=xj y conocemos la derivada de orden j-i en el punto xi de la función f a interpolar (naturalmente, será también fi=fi+1=...=fj),
con lo cuál podremos generalizar el método de Newton repitiendo r veces el punto (xi,fi) si conocemos las derivadas hasta el orden r-1 en xi (interpolación de Hermite).
Problema 13: Aplicar el método de Newton generalizado a partir de los datos p(0)=1, p'(0)=2, p(1)=3. Comprobar que el resultado obtenido es el polinomio de grado igual o inferior a 2 que cumple dichas condiciones.
Actividad 8. Asumiendo que el error de la interpolación polinómica de grado menor o igual que m viene dada por
Teorema -12: f(x)-pm(x) = [f (m+1)(ξ(x))/(m+1)!] ∏i=0 m (x-xi) tal que ξ(x)c[a,b] tal que para todo i=0,1...m, xic[a,b]
Problema 14: Acotar el valor de f(3) suponiendo que
| x
k |
1 |
2 |
4 |
5 |
| f(x
k) |
0 |
2 |
12 |
21 |
Tema 4. Obtener una solución aproximada de la integral definida de una función, ∫ab f(x)dx :
Objetivos:
- Obtener unos pesos Wk independientes de la función f(x) tales que sumando su producto por los correspondientes valores de la función en determinados nodos xk, ∑ i=0 m Wk f(xk), proporcione la integral exacta para polinomios hasta un cierto grado, y una buena aproximación para otras funciones.
- Aprender a acotar el error de dicha aproximación expresándolo como el producto de un factor C independiente de la función f(x) por la derivada de un cierto orden r de la función en algún punto ξ del intervalo de integración [a,b] , Cf(r)(ξ).
- Estudiar el caso de nodos equidistantes, xk=a+kh (Fórmula de Newton-Cotes).
- Aprender a mejorar la aproximación aumentando el
número de nodos.
- Aprender a mejorar la aproximación utilizando valores de la derivada de la función.
- Aprender a mejorar la aproximación escogiendo de forma adecuada los nodos (integración gaussiana).
- Aprender a valorar comparativamente distintos métodos teniendo en cuenta tanto su máximo error de aproximación como su coste de computación.
- Utilizar el método de coeficientes indeterminados para obtener tanto los pesos Wk como el factor C del error, a partir de la integral exacta de potencias simples y resolviendo en grupos pequeños los correspondientes sistemas de ecuaciones para exponer públicamente a continuación los resultados obtenidos.
- Aplicar las fórmulas obtenidas para aproximar la integral de determinadas funciones trabajando en grupos pequeños y exponiendo públicamente a continuación los resultados obtenidos.
- Trabajar en aula de informática elaborando programas para la aproximación de integrales por distintos métodos, valorando y comparando los resultados obtenidos.
Actividad 1. Teniendo en cuenta la
Definición 14: Siendo f:[a,b]→R una función integrable, llamaremos integral numérica polinómica de f en los nodos xk tales que a≤x0<...<xm≤b a la integral en el intervalo [a,b] del polinomio interpolador de grado menor o igual que m en los puntos {(xk,f(xk)}k=0,1...m
y utilizando la expresión del polinomio interpolador proporcionada por el Método de Lagrange, justificar la existencia de unos pesos Wk independientes de la función f(x) con los cuáles ∑ i=0 m Wk f(xk) sea su integral numérica polinómica.
Actividad 2. Teniendo en cuenta que una integral numérica polinómica en m+1 nodos es igual a la integral exacta para polinomios de grado menor o igual que m, encontrar un sistema de ecuaciones para la obtención de los pesos Wk y demostrar que si para todo i≠k, xi≠xk, dicho sistema de ecuaciones tiene solución única.
Actividad 3.
Deducir la fórmula de la integral numérica polinómica tomando como nodos los extremos del intervalo (Fórmula del Trapecio),
T=
Actividad 4.
Problema 15: Aplicar la Fórmula del Trapecio para obtener una aproximación a la integral de (1+x3)½ entre 0 y 10 (ver Figura en http://www.uv.es/pla/Tutoria/mniq/p15.gif).
Actividad 5. Teniendo en cuenta la expresión del error de la interpolación polinómica de grado menor o igual que m dada por el Teorema -12, así como que
Teorema -13: Para toda función integrable f:[a,b]→R, |∫ab f(x)dx| ≤ ∫ab |f(x)|dx .
Teorema -14: Para todo par de funciones integrables f:[a,b]→R, g:[a,b]→R+, existe ξc[a,b] tal que
Teorema 25: El valor absoluto del error de la integral numérica polinómica en m+1 nodos puede acotarse por el producto de dos factores, uno de los cuáles depende únicamente de los nodos, y el otro depende únicamente de la derivada de orden m+1 en algún punto ξ del intervalo de integración [a,b].
Actividad 6. Suponiendo que el error de un método de integración aproximada sea de la forma
NOTA: en caso de obtenerse C=0 puede inferirse que el método es exacto para dicha función, y deberá repetirse el proceso sustituyendo r por r+1 .
Actividad 7.
Obtener la expresión del error para la Fórmula del Trapecio,
εT =
Indicar para qué polinomios será exacta dicha fórmula.
Actividad 8.
Problema 16: Acotar ∫0 10 (1+x3)½dx sabiendo que |f "(x)|<1'468 en dicho intervalo.
Actividad 9. Teniendo en cuenta el
Teorema -15: ∫ab f(x) dx = ∫u-1(a) u-1(b) f(u(t)) u'dt
demostrar el
Teorema 26: En el caso de nodos equidistantes x k=a+kh, con k=0,1...m, h=(b-a)/m, demostrar que los pesos para el cálculo de la correspondiente integral numérica polinómica (pesos de Newton-Cotes) tienen la forma Wk=hW'k(m), donde W'k(m), que son los pesos correspondientes al caso h=1, sólo dependen de k y de m (pero no de a y de b).
Puede utilizarse para la demostración la expresión de los pesos Wk obtenida en la Actividad 1, aplicando en la correspondiente integral el cambio de variable x=a+th .
Actividad 10. Obtener los pesos de Newton-Cotes para m=2 y el intervalo [0,2]. A partir de los mismos, obtener la fórmula general (Fórmula de Simpson) para la integral numérica polinómica en los nodos {a, a+h, a+2h} = {a, (a+b)/2, b},
S =
Actividad 11.
Problema 17: Aproximar mediante la Fórmula de Simpson ∫-1 1 e x2 dx .
Actividad 12.
Teniendo en
cuenta el
| Teorema -16:
Para todo fcC
r(R→R),
xcC1(R→R),
|
dr f
dtr |
(x(t)) = ﴾dx/dt﴿r
|
dr f
dxr |
(x) |
Teorema 27: Si la expresión del error para aproximar ∫0 m f(t)dt con nodos equidistantes y h=1 es
| ε' = C' | dr f dtr |
(ζ) para
algún ζc[0,m], |
| ε = C | dr f dxr |
(ξ) para algún ξc[a,b] con C=hr+1 C' |
Actividad 13. Obtener la expresión del error para la Fórmula de Simpson para el intervalo [0,2] (con h=1), y a partir de ella obtener la expresión general del error para la Fórmula de Simpson para el intervalo [a,b] (con h=(b-a)/2),
εS =
Indicar para qué polinomios será exacta dicha fórmula.
Actividad 14.
Problema 18: Acotar el error de la Fórmula de Simpson aplicada a ∫-1 1 e x2 dx . Valorarlo.
Actividad 15. Teniendo en cuenta la
Definición 15: Siendo f:[a,b]→R una función integrable, llamaremos integral numérica compuesta de grado m en los mM+1 nodos {a+kh}k=0,1...mM , con h=(b-a)/(mM), a
demostrar el
Teorema 28: Para toda función integrable f:[a,b]→R , su integral numérica compuesta de grado 2 en los 2M+1 nodos {a+kh}k=0,1...2M , con h=(b-a)/(2M) (regla de Simpson), viene dada por
= [f(a) + f(b) + ∑i=1 M-1 2f(a+2ih) + ∑i=0 M-1 4f(a+(2i+1)h)](b-a)/(6M)
Actividad 16. Teniendo en cuenta el
Teorema -17: Para toda función continua f:[a,b]→R y todo conjunto de puntos ξ ic[a,b], i=1...n, existe ξc[a,b] tal que
Teorema 29: Para toda fcC4([a,b],R), el error de la regla de Simpson para aproximar ∫ab f(x)dx viene dado por
Actividad 17.
Problema 19: ¿Qué incremento h deberemos tomar para obtener una aproximación a ∫-1 1 e x2 dx con un error menor a 0'01 mediante la regla de Simpson?
Actividad 18.
Calcular los
pesos adecuados para que W'0
f(0)+W'1
f(1)+W'2 f
'(0)+W'3
f '(1) nos dé el valor exacto de
∫0 1
f(t)dt para polinomios hasta
el tercer grado. A partir de dichos pesos, y teniendo en cuenta el
Teorema -18:
Para todo
fcC
r(R→R),
xcC1(R→R),
df/dt = (df/dx)·(dx/dt) ,
obtener la fórmula general (Fórmula
del Trapecio Corregida) que resulta de sustituir la
integral ∫ab
f(x)dx por la integral del polinomio interpolador de Hermite para el
que coinciden los valores de la función y de su primera derivada
en los extremos del intervalo,
TC=
Comparar con la fórmula obtenida en la Actividad 3 y justificar
por qué se llama Fórmula del Trapecio Corregida. ¿En qué
caso ambas fórmulas coincidirán?
Actividad 19.
Obtener la
expresión del error para la Fórmula del Trapecio
Corregida para el
intervalo [0,1] (con h=1), y a partir de ella obtener la
expresión
general del error para la Fórmula del Trapecio Corregida para el
intervalo [a,b]
(con h=b-a),
εTC
=
Indicar para qué polinomios será exacta dicha
fórmula.
Actividad 20.
Problema 20:
Acotar ∫0 10
(1+x3)½dx
sabiendo que |f (4)(x)|<10
en dicho
intervalo (ver Figura en http://www.uv.es/pla/Tutoria/mniq/p15.gif).
Actividad 21.
Demostrar el
Teorema 30:
Para toda fcC4([a,b],R),
Actividad 22. Teniendo en cuenta que el coste computacional del cálculo numérico aproximado de una integral puede medirse por el número de veces que se evalúa la función f(x) o su derivada f '(x), comparar el coste computacional de la regla de Simpson y la regla del Trapecio Corregida con el mismo valor de M. ¿Cuál sería el coste computacional de la regla de Simpson con M=11? ¿Para qué valor de M la regla del Trapecio Corregida tendría el mismo coste computacional? Comparar la estimación de los errores de ambas reglas con el mismo coste computacional.
Actividad 23.
Problema 21: ¿Qué incremento h deberemos tomar para obtener una aproximación a ∫-1 1 e x2 dx con un error menor a 0'01 mediante la regla del Trapecio Corregida? Comparar su coste computacional con el del Problema 19 (Actividad 17).
¿En qué casos será preferible utilizar la regla del Trapecio Corregida?
Actividad 24.
Calcular los
pesos W'0 y W'1
y
el valor de c
para los
cuáles W'0 f(-c) + W'1
f(c) da el valor exacto de
∫-1 1 f(t)dt
para polinomios
hasta el segundo grado. Comprobar que {-c, c} son las raíces del polinomio de Legendre
de 2º grado, P2(t)=(3t2-1)/2,
que cumple las condiciones de ortogonalidad
∫-1 1 P2(t)P1(t)dt
= 0
∫-1 1 P2(t)P0(t)dt
= 0
con P0(t)=1 y P1(t)=t
polinomios de Legendre que cumplen a su vez
∫-1 1 P1(t)P0(t)dt
= 0
Actividad 25.
Obtener la
expresión del error de la integral numérica
polinómica de ∫-1 1
f(t)dt
en las raíces del polinomio de Legendre de 2º grado.
Indicar para qué polinomios será exacto dicho
método.
Actividad 26.
Obtener una
fórmula general para la integración de ∫ab
f(x)dx realizando el cambio x=(a+b)/2 + (b-a)t/2 y utilizando la
integral numérica polinómica de ∫-1 1
f(t)dt en las raíces del polinomio de
Legendre de
2º grado,
L2 =
con un error
εL2
=
Actividad 27.
Problema 22:
Aproximar, utilizando la fórmula derivada de la
integración numérica polinómica en las
raíces del polinomio de Legendre de 2º grado,
a) ∫-1
1
e x2 dx
b) ∫0 10
(1+x3)½dx
Acotar los correspondientes errores.
Actividad 28.
Demostrar el
Teorema 31:
Para toda fcC4([a,b],R),
Trabajo 4 (para su realización en equipo):
Obtener los coeficientes W0, W1, W2 y W3 que hacen que