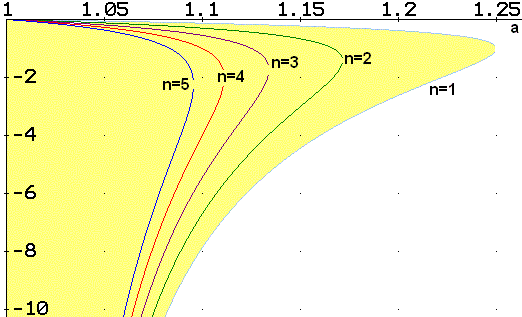
Figura 3.1
Intervals de m on es podria vulnerar la condició
de proporcionalitat estricta si a<(n+2)/(n+1)
Essent
Para n<(2-a)/(a-1) aquests arrels són negatius, com es mostra en la Figura 3.1.

Figura 3.1
Intervals de m on es podria vulnerar la condició
de proporcionalitat estricta si a<(n+2)/(n+1)
Per tant, i com m ha de ser enter positiu, la condició de proporcionalitat s'acompleix sempre que
La Figura 3.2 mostra, per a diferents valor de a i n, intervals de m on es pot vulnerar la condició de proporcionalitat estricta.
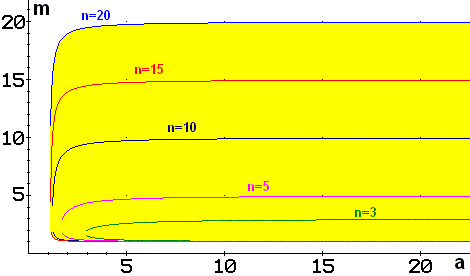
Figura 3.2
Intervals de m on es pot vulnerar la condició
de proporcionalitat estricta
La proporcionalitat estricta no es podrà vulnerar si el discriminant de l'equació de segon grau en m és sempre negatiu, cosa que es produirà si n < [a+2Ö(a-1)]/(a-1) (zona colorejada de la Figura 3).
Així mateix, la vulneració de la proporcionalitat estricta requerirà un número mínim de candidatures, r ³ a/(a-1) + n/m