Una aproximació general a la probabilitat la defineix com la possibilitat d'ocurrència d'un esdeveniment. El comportament no es un fenomen absolutament previsible, ni determinat, i per esta raó la probabilitat és molt apropiada per quantificar la possibilitat d'observar comportaments o característiques del comportament. Un primer ús de la probabilitat consisteix en la quantificació de la possibilitat d'ocurrència de comportaments o característiques d'interès.

Un altre ús de la probabilitat consisteix en la modelització de l'efecte de l'atzar, que comparat en distribucions de les dades fa possible decidir si allò que observem es explicable a l'atzar. Bona part dels procediments d'estadística inferencial es basen en la comparació de les distribucions observades amb models de distribucions aleatòries de probabilitat. Els models habitualment utilitzats en la investigació psicològica són el binomial per variables discretes, y el normal, t, Khi quadrat i F per variables contínues.

Alguns conceptes bàsics

La probabilitat pot ser definida des de vessants diferents. L'aproximació freqüentista defineix la probabilitat d'ocurrència d'un esdeveniment A (a més d'altres definicions) com la raó entre la freqüència de A (nombre de vegades que és observat) i el nombre de vegades que pot ocórrer:

 

En algunes situacions podem obtenir una aproximació raonable a la probabilitat. Per exemple, la que un estudiant seleccionat a l'atzar obtinga "Notable" a la fi del curs. Esta probabilitat és el nombre d'estudiants que obtenen "Notable" dividit pel nombre total d'estudiants del curs:

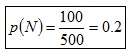
Direm que la probabilitat que un estudiant seleccionat a l'atzar obtinga Notable és de 0.2 (donat que 100 estudiants han obtingut Notable en un curs amb 500 estudiants).

 

Altres regles bàsiques de la probabilitat són:

Regla de l'adició: si dos esdeveniments A i B són mútuament exhaustius i excloents, la probabilitat d'ocurrència de A o B és la suma de les probabilitats simples:

Regla del producte: si dos esdeveniments A i B són independents, la probabilitat de que ocorrega A i ocorrega B és igual al producte de les probabilitats simples:

 

Teorema de Bayes

El teorema de Bayes és una expressió per obtenir probabilitats condicionals (probabilitats d'ocurrència d'esdeveniments condicionades a l'ocurrència d'uns altres esdeveniments). L'expressió del teorema de Bayes per a dues variables discretes és:

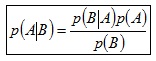
Per variables que prenen més de dos valors, l'expressió és:

El teorema de Bayes dóna resposta a qüestions de tipus causal, predictives i de diagnòstic. En les qüestions causals volem saber quina és la probabilitat d'esdeveniments que són la conseqüència d'uns altres esdeveniments. En les qüestions predictives volem saber quina és la probabilitat d'esdeveniments donada informació de l'ocurrència dels esdeveniments predictors. En les qüestions de tipus diagnòstic volem saber quina és la probabilitat de l'esdeveniment (o esdeveniments) causals o predictius donat que en tenim informació de les conseqüències. Per resumir, de les situacions causals o predictives en desconeixem les conseqüències i en tenim evidència de les causes. Per contra, de les situacions de diagnòstic en desconeixem les causes i en tenim evidència de les conseqüències.

Exemple

Uns psicòlegs especialitzats en el tractament de trastorns de personalitat estan interessats a diagnosticar el trastorn que afecta un pacient, en qui observen un conjunt de símptomes que indiquen que podria patir el trastorn A o el trastorn B. A més d'això, saben que els percentatges d'individus afectats pels trastorns A, B o cap trastorn són 10, 30 i 70, respectivament. També saben que el percentatge d'individus afectats pel trastorn A i que mostren el símptoma X és del 60%, el percentatge d'individus que pateixen el trastorn B i mostren el símptoma X és del 30% i el percentatge d'individus no afectats que mostren els símptomes de trastorn és del 10%. En resum, la informació de què disposem és:

Substituim al teorema de Bayes:

la probabilitat que l'individu patisca el trastorn A és de 0.29. Les probabilitats que estiga afectat pel trastorn B i que no estiga afectat per cap trastorn són:

La conclusió més probable és que l'individu patisca el trastorn B, però és un valor moderat i els psicòlegs pensen que cal obtenir-ne evidències noves.

El teorema de Bayes és especialment adequat per actualitzar les conclusions a mesura que disposem d'informació nova. Passat un temps, observen que el pacient mostra un símptoma nou (Y) i saben que mostren Y el 70% dels individus que pateixen el trastorn A, el 20% dels individus que pateixen el trastorn B i el 10% dels individus que no pateixen cap trastorn. Per obtenir les probabilitats en incorporar la informació nova fem que les probabilitats posteriors que hem obtingut passen a ser les probabilitats prèvies:

Una vegada fets els càlculs, veiem que la probabilitat que l'individu estiga afectat pel trastorn A ha passat de 0.27 a 0.63